131 – 140. Найти общее решение дифференциального уравнения.
131. а). 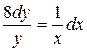 ; б).
; б). 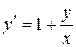 ; в).
; в).  .
.
132. а). 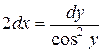 ; б).
; б). 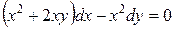 ; в).
; в). 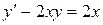 .
.
133. а).  ; б).
; б).  ; в).
; в). 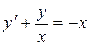 .
.
134. а).  ; б).
; б). 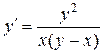 ; в).
; в). 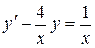 .
.
135. а).  ;б).
;б). 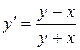 ; в).
; в). 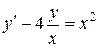 .
.
136. а).  ; б).
; б).  ; в).
; в). 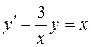 .
.
137. а).  ; б).
; б).  ; в).
; в). 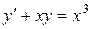 .
.
138. а). 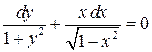 ; б).
; б). 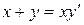 ; в).
; в). 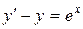 .
.
139. а). 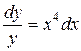 ; б).
; б). 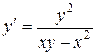 ; в).
; в). 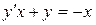 .
.
140. а). 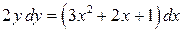 ; б).
; б).  ; в).
; в).  .
.
Пример.
а) 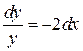 .
.
Данное уравнение является уравнением с разделенными переменными. Проинтегрируем обе его части:
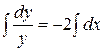 , получим:
, получим:  .
.
б). 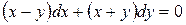 .
.
Для решения данного уравнения используем тот факт, что  . Так как переменные в данном случае разделить нельзя, то выразим
. Так как переменные в данном случае разделить нельзя, то выразим 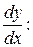
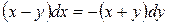 , отсюда по правилу пропорции получаем:
, отсюда по правилу пропорции получаем:
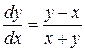 , или
, или  .
.
В данном случае 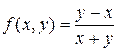 ;
; 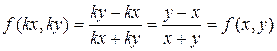 .
.
Следовательно, данное уравнение – однородное. Делаем замену переменной
 ,
, 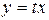 ,
,  . После замены получим:
. После замены получим:
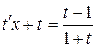 ,
, 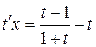 ,
, 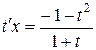 .
.
Получили уравнение с разделяющимися переменными. Разделяя переменные, получим:  ,
,  .
.
Интегрируя, находим общее решение
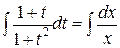 ,
, 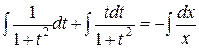 ,
,
 .
.
Возвращаясь к старой переменной, получаем общий интеграл
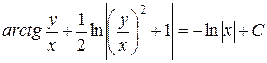 .
.
в). 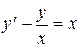 .
.
Данное уравнение линейное. Ищем решение в виде 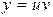 ,
,  .
.
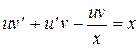 ,
, 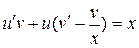 .
.
Решаем уравнение. 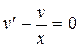 ,
, 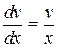 ,
,  ,
,  ,
, 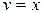 .
.
Подставляя полученное значение  в уравнение, имеем:
в уравнение, имеем:
 ,
, 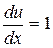 ,
,  .
.
Общее решение  или
или 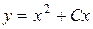 .
.
 ,
, 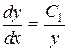 ,
, 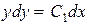 ,
, 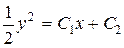 .
.
141–150. Найти общее решение дифференциального уравнения:
141. а). 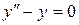 ; б).
; б).  ; в).
; в). 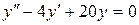 .
.
142. а).  ; б).
; б). 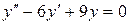 ; в).
; в). 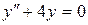 .
.
143. а). 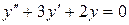 ; б).
; б). 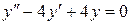 ; в).
; в).  .
.
144. а). 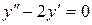 ; б).
; б). 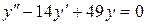 ; в).
; в).  .
.
145. а). 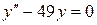 ; б).
; б).  ; в).
; в).  .
.
146. а).  ; б).
; б). 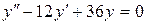 ; в).
; в). 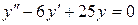 .
.
147. а). 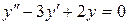 ; б).
; б). 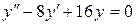 ; в).
; в).  .
.
148. а). 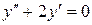 ; б).
; б).  ; в).
; в).  .
.
149. а).  ; б).
; б). 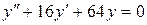 ; в).
; в). 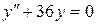 .
.
150. а). 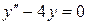 ; б).
; б). 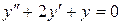 ; в).
; в). 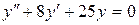 .
.
Пример. а). 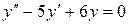 .
.
Составим соответствующее характеристическое уравнение:
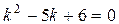 ,
,
 ,
,  .
.
Так как корни характеристического уравнения 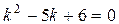 действительные, различные, следовательно, общее решение однородного уравнения имеет вид
действительные, различные, следовательно, общее решение однородного уравнения имеет вид 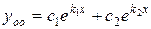 , то есть имеем
, то есть имеем
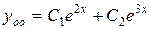 .
.
б). 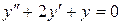 .
.
Составим соответствующее характеристическое уравнение:
 ,
,
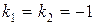 .
.
Так как корни характеристического уравнения  действительные, одинаковые, следовательно, общее решение однородного уравнения имеет вид
действительные, одинаковые, следовательно, общее решение однородного уравнения имеет вид 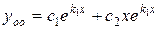 , то есть имеем
, то есть имеем
 .
.
в). 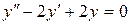 .
.
Составим соответствующее характеристическое уравнение:
 . Решим его при помощи вычисления дискриминанта:
. Решим его при помощи вычисления дискриминанта:
 . Так как в данном случае
. Так как в данном случае 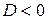 , то для вычисления квадратного корня
, то для вычисления квадратного корня  используем равенство
используем равенство 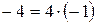 . Так как
. Так как 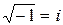 (комплексная единица), то в данном случае
(комплексная единица), то в данном случае  . Таким образом, имеем в данном случае комплексные корни:
. Таким образом, имеем в данном случае комплексные корни:
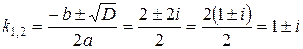 .
.
Так как корни характеристического уравнения  комплексно-сопряженные, следовательно, общее решение однородного уравнения имеет вид
комплексно-сопряженные, следовательно, общее решение однородного уравнения имеет вид 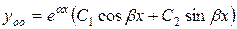 , где
, где 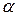 и
и 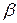 - соответственно действительная и мнимая части комплексных корней. В данном случае
- соответственно действительная и мнимая части комплексных корней. В данном случае 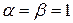 . Таким образом, общее решение исходного уравнения имеет вид:
. Таким образом, общее решение исходного уравнения имеет вид:
 .
.
 2017-10-25
2017-10-25 469
469







