101-110. Найти неопределённые интегралы.
101. а).  ; б).
; б).  ; в).
; в).  .
.
102. а). 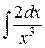 ; б)
; б)  ; в).
; в).  .
.
103. а).  ; б)
; б) 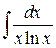 ; в).
; в).  .
.
104. а). 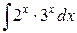 ; б)
; б)  ; в).
; в). 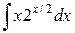 .
.
105. а).  ; б)
; б)  ; в).
; в). 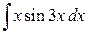 .
.
106. а)  ; б)
; б)  ; в)
; в) 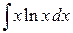 .
.
107. а)  ; б)
; б)  ; в)
; в)  .
.
108. а)  ; б)
; б)  ; в)
; в)  .
.
109. а)  ; б)
; б)  ; в)
; в) 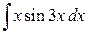 .
.
110. а)  ; б)
; б)  ; в)
; в)  .
.
Пример. Найти неопределённые интегралы.
а)  ; б)
; б)  ; в)
; в)  .
.
а) Данный интеграл не является табличным. Поэтому предварительно сделаем элементарные математические преобразования, в данном случае воспользовавшись формулой сокращенного умножения, а потом таблицей интегралов основных элементарных функций, получим:

б) пусть требуется найти интеграл вида 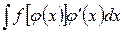 , где подынтегральная функция непрерывна. Сделаем замену
, где подынтегральная функция непрерывна. Сделаем замену  , тогда
, тогда  . Получим
. Получим  . В найденном интеграле перейдем к прежней переменной
. В найденном интеграле перейдем к прежней переменной  , воспользовавшись равенством
, воспользовавшись равенством  .
.
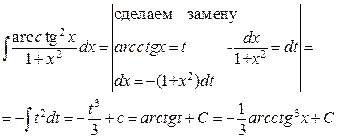 .
.
в)  . Имеем интеграл вида
. Имеем интеграл вида  . Применим формулу интегрирования по частям
. Применим формулу интегрирования по частям  :
:

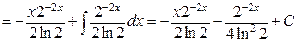 .
.
111-120. Вычислить определенные интегралы
111. а)  ; б)
; б) 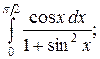 в)
в)  .
.
112. а) 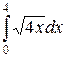 ; б)
; б) 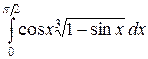 ; в)
; в)  .
.
113. а)  ; б)
; б)  в)
в) 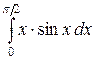 .
.
114. а)  ; б)
; б)  в)
в) 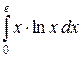 .
.
115. а)  ; б)
; б)  в)
в)  .
.
116. а) 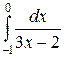 ; б)
; б)  в)
в)  .
.
117. а)  ; б)
; б)  ; в)
; в) 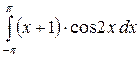 .
.
118. а)  ; б)
; б)  в)
в) 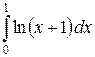 .
.
119. а)  ; б)
; б)  в)
в)  .
.
120. а)  ; б)
; б)  в)
в) 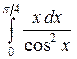 .
.
Пример.
а)  . Применяя формулу Ньютона-Лейбница, вычислим этот интеграл:
. Применяя формулу Ньютона-Лейбница, вычислим этот интеграл:
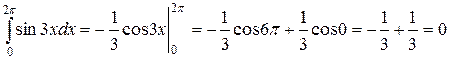
б) 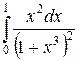 . Вычислим этот интеграл, используя метод замены переменной:
. Вычислим этот интеграл, используя метод замены переменной:
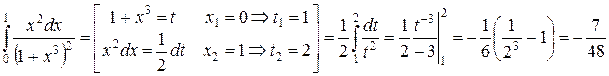
в)  . Применяя формулу интегрирования по частям получим:
. Применяя формулу интегрирования по частям получим:

121.-130. Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.
121.  ,
, 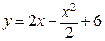 . 126.
. 126. 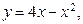

122.  ,
,  . 127.
. 127. 
123. 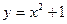 ,
,  . 128.
. 128. 
124. 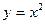 ,
,  . 129.
. 129. 
125. 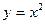 ,
, 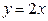 . 130.
. 130. 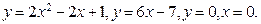
Пример.
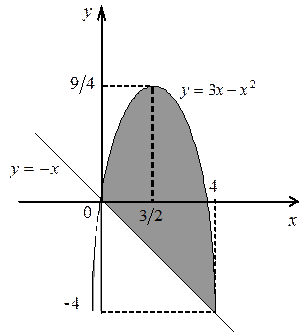
а) Вычислить площадь фигуры, ограниченной параболой 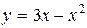 и прямой
и прямой  .
.
Находим точки пересечения данных кривых и строим искомую фигуру


Площадь фигуры, ограниченной снизу кривой 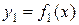 , сверху – кривой
, сверху – кривой 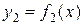 , вычисляет интеграл
, вычисляет интеграл  , где
, где  и
и  - абсциссы точек пересечения этих кривых, причем
- абсциссы точек пересечения этих кривых, причем 
Следовательно, имеем
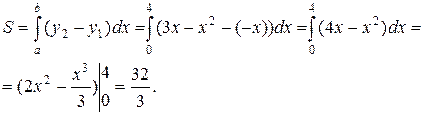
 2017-10-25
2017-10-25 686
686








