1-10. Даны координаты вершин треугольника  . Найти: 1) Длины сторон треугольника; 2) Внутренний угол при вершине A треугольника; 3) Уравнение прямой BC; 4) Уравнение высоты, опущенной из вершины A; 5) Уравнение прямой, проходящей через вершину A, параллельно стороне BC.
. Найти: 1) Длины сторон треугольника; 2) Внутренний угол при вершине A треугольника; 3) Уравнение прямой BC; 4) Уравнение высоты, опущенной из вершины A; 5) Уравнение прямой, проходящей через вершину A, параллельно стороне BC.
1. 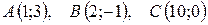 .
.
2. 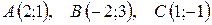 .
.
3. 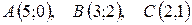 .
.
4. 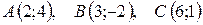 .
.
5. 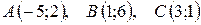 .
.
6. 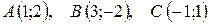 .
.
7. 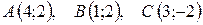 .
.
8. 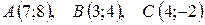 .
.
9. 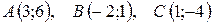 .
.
10. 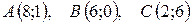 .
.
Пример. 
1) Найдем сначала координаты векторов 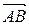 ,
, 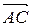 и
и 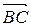 . Для этого из координат конца вектора вычитаем координаты его начала:
. Для этого из координат конца вектора вычитаем координаты его начала:
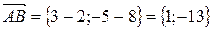 .
.
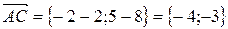 .
.
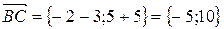 .
.
Модуль вектора (равный расстоянию между точками A и B, A и C, B и C) представляет собой корень из суммы квадратов координат соответствующего вектора:
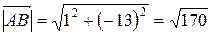 .
.
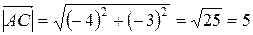 .
.
 .
.
2) Внутренний угол при вершине A треугольника найдем как угол между сторонами AB и AC треугольника. Этот угол равен углу между векторами 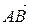 и
и 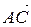 и находится по формуле:
и находится по формуле:
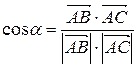 .
.
Тогда 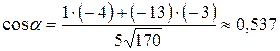 ;
; 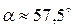 .
.
3) Уравнение прямой BC запишем используя уравнение прямой, проходящей через две точки с координатами 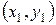 и
и 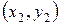 :
:
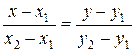 .
.
Подставляя значения координат точек B и C, получим
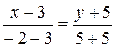 .
.
После приведения подобных получим уравнение прямой BC:
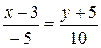 .
.
4) Высота, опущенная из вершины 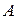 , перпендикулярна стороне
, перпендикулярна стороне 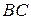 . Следовательно скалярное произведение вектора, лежащего на высоте (будем обозначать его
. Следовательно скалярное произведение вектора, лежащего на высоте (будем обозначать его 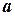 ) и вектора
) и вектора 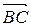 равно нулю. Вектор
равно нулю. Вектор 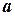 имеет координаты
имеет координаты 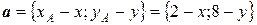 , где x и y – координаты произвольной точки, лежащей на высоте. Запишем скалярное произведение
, где x и y – координаты произвольной точки, лежащей на высоте. Запишем скалярное произведение 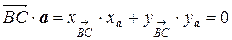 :
:
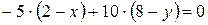 .
.
После раскрытия скобок и приведения подобных получим
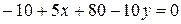 ;
;
 .
.
Это и есть искомое уравнение высоты.
5) Вектор 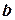 , параллельный стороне
, параллельный стороне 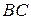 , имеет координаты
, имеет координаты 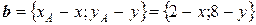 , где x и y – координаты произвольной точки этого вектора. Из условия параллельности векторов
, где x и y – координаты произвольной точки этого вектора. Из условия параллельности векторов 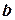 и
и 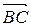 следует
следует 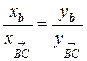 . Подставляя в это соотношение координаты соответствующих векторов и приводя подобные получим
. Подставляя в это соотношение координаты соответствующих векторов и приводя подобные получим
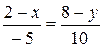 ;
; 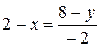 ;
;
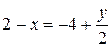 ;
; 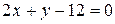 .
.
11-20. Даны координаты вершин пирамиды A1A2A3A4. Найти: 1) длину ребра A1A2; 2) угол между ребрами A1A2 и A1A4; 3) площадь грани A1A2A3; 4) объем пирамиды; 5) уравнение плоскости A1A2A3; 6) уравнения прямой A1A4; 7) Угол между ребром A1A4 и гранью A1A2A3; 8) уравнение высоты, опущенной из вершины A4 на плоскость A1A2A3.
11. 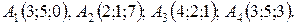
12. 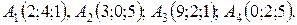
13. 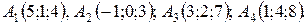
14. 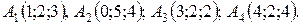
15. 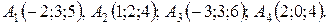
16. 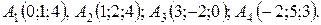
17. 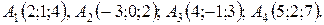
18. 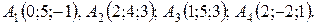
19. 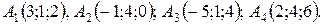
20. 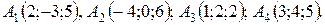
Пример. 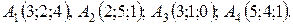
Если точка 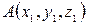 - начало вектора, а точка
- начало вектора, а точка 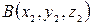 - его конец, то координаты вектора находятся по формулам
- его конец, то координаты вектора находятся по формулам
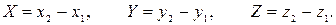
1) Найдем сначала координаты вектора 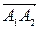 :
:
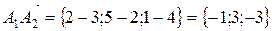 .
.
Модуль вектора (равный расстоянию между точками A1 и A2)представляет собой корень из суммы квадратов координат вектора:
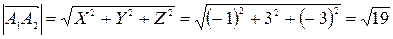 .
.
2) Угол между ребрами A1A2 и A1A4 равен углу между соответствующими векторами и находится по формуле:
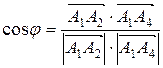 , где
, где 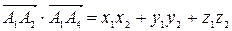 - скалярное произведение векторов, записанное в координатной форме.
- скалярное произведение векторов, записанное в координатной форме.
Координаты вектора 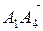 равны:
равны:
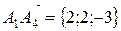 ,
, 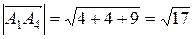 .
.
Тогда 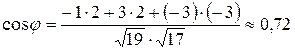 ;
; 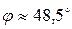 .
.
3) Уравнение плоскости, проходящей через три заданные точки 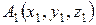 ,
, 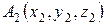 ,
, 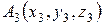 , имеет вид:
, имеет вид:
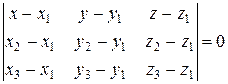 .
.
Подставляя значения координат, вычисляем определитель:
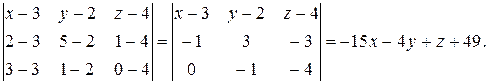
Итак, искомое уравнение плоскости имеет вид
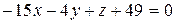 или
или 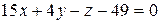 .
.
4) Уравнения прямой, проходящей через точки 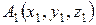 и
и 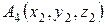 , имеет вид
, имеет вид
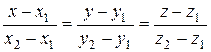 .
.
Таким образом, получаем искомые уравнения:
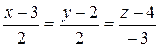 .
.
5) Если даны плоскость 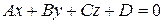 с нормальным вектором
с нормальным вектором 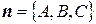 и прямая
и прямая 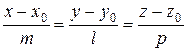 с направляющим вектором
с направляющим вектором 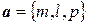 , то угол между прямой и плоскостью определяется по формуле
, то угол между прямой и плоскостью определяется по формуле
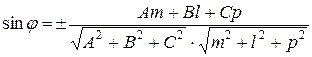 .
.
Так как 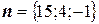 , а
, а 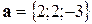 , то
, то
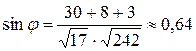 ,
, 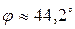 .
.
6) Площадь треугольника, построенного на двух векторах, равна половине модуля векторного произведения этих векторов:
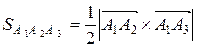 , где
, где 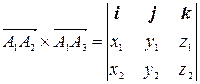 - векторное произведение векторов.
- векторное произведение векторов. 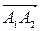 и
и 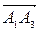 .
.
Так как
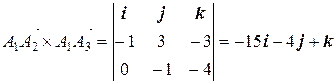 ,
,
то
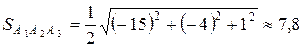 (кв. ед.).
(кв. ед.).
7) Объем пирамиды, построенной на трех векторах, равен одной шестой модуля смешанного произведения этих векторов:
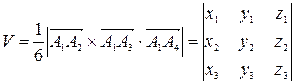 .
.
Следовательно,
 (куб. ед.)
(куб. ед.)
8) Так как в качестве направляющего вектора прямой, проходящей через заданную точку D перпендикулярно плоскости ABC, можно выбрать вектор нормали n к плоскости, то канонические уравнения искомой прямой запишется в виде
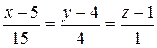 .
.
Пример.2. Из точки P(2;3;-5) на координатные плоскости опущены перпендикуляры. Найти уравнение плоскости, проходящей через их основания.
Основаниями перпендикуляров, опущенных из точки P(2;3;-5) на координатные плоскости, служат точки P1(2;3;0), P2(2;0;-5) и P3(0;3;-5). требуется составить уравнение плоскости, проходящей через три заданные точки.
Чтобы найти нормальный вектор плоскости, рассмотрим два вектора 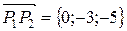 и
и 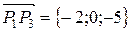 . Они лежат в искомой плоскости, значит,
. Они лежат в искомой плоскости, значит, 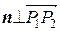 и
и 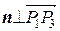 . Следовательно,
. Следовательно,
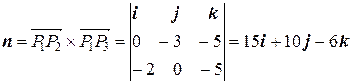 ,
,
Уравнение искомой плоскости, проходящей через точку M1(x1, y1, z1) перпендикулярно вектору 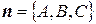 , имеет вид
, имеет вид 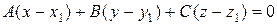 :
:
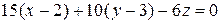 ;
;
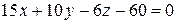 .
.
в) Составить канонические уравнения прямой
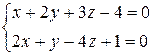
Чтобы найти какую – либо точку, принадлежащую прямой, зафиксируем одну переменную, например z, положив z = 0, и решим полученную систему двух уравнений с двумя неизвестными
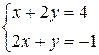
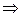
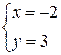
Таким образом, одна из точек, принадлежащих прямой, имеет координаты 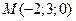 .
.
Теперь найдем направляющий вектор прямой. Так как 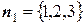 и
и 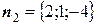 , то
, то
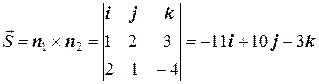 .
.
Канонические уравнения прямой запишутся в виде:
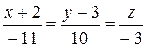 .
.
 2017-10-25
2017-10-25 1233
1233








