Для завдання лінійного коду використається також інший спосіб. Він заснований на тім, що у всякому підпросторі лінійного простору можна вибрати базис, тобто таку лінійно незалежну систему з 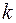 векторів
векторів 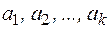 , що складаються з
, що складаються з 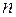 компонентів кожний, через які лінійно виражаються всі взагалі вектори підпростору. Таким чином, система базисних векторів
компонентів кожний, через які лінійно виражаються всі взагалі вектори підпростору. Таким чином, система базисних векторів 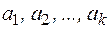 повністю визначає лінійний (
повністю визначає лінійний (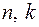 )-код. Матриця
)-код. Матриця 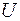 , складена з них,
, складена з них,
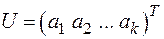 , (5)
, (5)
називається утворюючою матрицею коду.
При заданій інформаційній комбінації 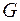 відповідна кодова комбінація буде визначатися виразом:
відповідна кодова комбінація буде визначатися виразом:
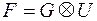 . (6)
. (6)
Утворююча матриця циклічного (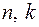 )-коду складається з одиничної матриці
)-коду складається з одиничної матриці 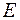 , що містить k рядків й k стовпців, і матриці доповнень
, що містить k рядків й k стовпців, і матриці доповнень 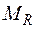 , що містить
, що містить 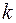 рядків і
рядків і  стовпців:
стовпців:
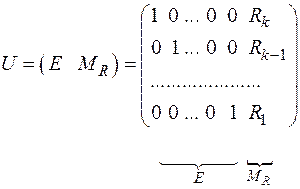 . (7)
. (7)
Рядками матриці доповнень 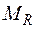 є k m- розрядних часткових залишків
є k m- розрядних часткових залишків 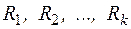 від розподілу одиниці з
від розподілу одиниці з 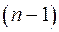 нулями на утворюючий многочлен, причому перший залишок записується у останньому рядку, а останній – у першому.
нулями на утворюючий многочлен, причому перший залишок записується у останньому рядку, а останній – у першому.
Як відзначалося, рядки утворюючої матриці є вихідними лінійно незалежними кодовими комбінаціями 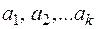 . Всі інші кодові комбінації циклічного коду створюються або відповідно до виразу (6), або підсумовуванням по модулю 2усіляких варіантів вихідних кодових комбінацій
. Всі інші кодові комбінації циклічного коду створюються або відповідно до виразу (6), або підсумовуванням по модулю 2усіляких варіантів вихідних кодових комбінацій 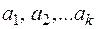 .
.
Приклад. Знайти утворюючу матрицю циклічного коду (7,4), якщо утворюючиймногочлен 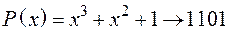 . Записати кодову комбінацію для інформаційної частини
. Записати кодову комбінацію для інформаційної частини 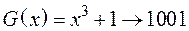 .
.
1 Записуємо одиничну матрицю розміром 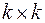 :
:
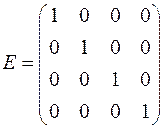 .
.
2 Розраховуємо матрицю доповнень розміром 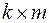 :
:
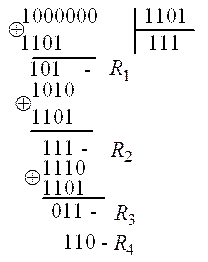
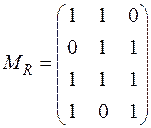 .
.
3 Записуємо утворюючу матрицю:
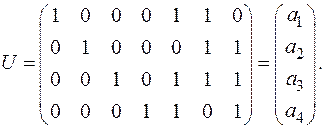
4 Знаходимо кодову комбінацію для вектора 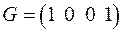 :
:
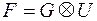 =
=
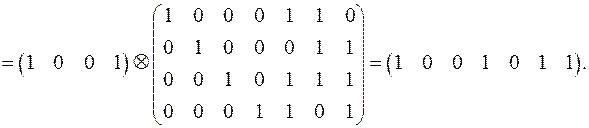
Виходячи зі структури вектора 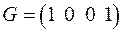 , можна також знайти кодову комбінацію шляхом додавання першої та четвертої вихідних лінійно незалежних кодових комбінацій:
, можна також знайти кодову комбінацію шляхом додавання першої та четвертої вихідних лінійно незалежних кодових комбінацій:
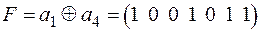 .
.
 2017-11-01
2017-11-01 882
882








