Циклічні коди відносяться до лінійних систематичних розподільних кодів. Вони мають фіксовані кількість розрядів і місце розташування інформаційної й контрольної частин. При загальній довжині кодової комбінації 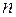 розрядів і довжині інформаційної частини
розрядів і довжині інформаційної частини 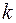 розрядів код позначається як
розрядів код позначається як 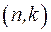 код. Структура
код. Структура 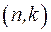 коду має такий вигляд:
коду має такий вигляд:
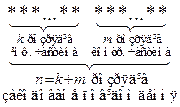 .
.
Циклічні коди будуються на основі операцій з інформаційними 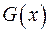 і утворюючим
і утворюючим 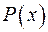 поліномами (многочленами) у кінцевому полі двійкових чисел. Умовне подання двійкового коду у вигляді полінома полягає в заміні підстави 2 на фіктивну змінну х. Наприклад, коду 10101001 відповідає поліном
поліномами (многочленами) у кінцевому полі двійкових чисел. Умовне подання двійкового коду у вигляді полінома полягає в заміні підстави 2 на фіктивну змінну х. Наприклад, коду 10101001 відповідає поліном
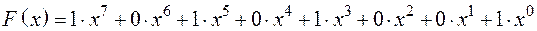 . (1)
. (1)
Як інформаційні поліноми 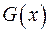 використаються кодові комбінації двійкового коду на всі сполучення, кількість комбінацій N якого при k інформаційних розрядах дорівнює
використаються кодові комбінації двійкового коду на всі сполучення, кількість комбінацій N якого при k інформаційних розрядах дорівнює
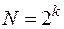 . (2)
. (2)
Утворюючий поліном 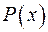 циклічного коду вибирається із числа многочленів, які не приводяться, тобто діляться без залишку тільки на себе або на одиницю. Деякі многочлени, які не приводяться, і їхні двійкові еквіваленти наведені в табл. 3.
циклічного коду вибирається із числа многочленів, які не приводяться, тобто діляться без залишку тільки на себе або на одиницю. Деякі многочлени, які не приводяться, і їхні двійкові еквіваленти наведені в табл. 3.
Таблиця 3 – Деякі многочлени, які не приводяться,
і їхні двійкові еквіваленти
| х + 1 →11 | х 4 + х + 1 →10011 |
| х 2 + х + 1 →111 | х 4 + х 3 + 1 →11001 |
| х 3 + х + 1 →1011 | 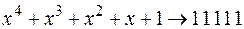 |
| х 3 + х 2 + 1 →1101 | 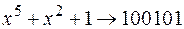 |
Ступінь m утворюючого полінома 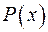 дорівнює кількості перевірочних (контрольних) розрядів і визначає мінімальну кодову відстань, а, отже, здатності циклічного коду з корекції помилок.
дорівнює кількості перевірочних (контрольних) розрядів і визначає мінімальну кодову відстань, а, отже, здатності циклічного коду з корекції помилок.
З метою утворення розподільних (систематичних) кодів, у яких контрольні розряди приписуються наприкінці коду після інформаційних символів, при формуванні циклічного коду кодова комбінація 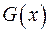 двійкового коду спочатку помножується на одночлен хm, що має той же ступінь, що й утворюючий поліном
двійкового коду спочатку помножується на одночлен хm, що має той же ступінь, що й утворюючий поліном 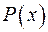 . Як відомо, множення
. Як відомо, множення 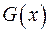 ∙ хm приводить до зсуву інформаційного полінома
∙ хm приводить до зсуву інформаційного полінома 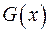 на m розрядів уліво (приписування наприкінці комбінації m нулів). Надалі додана частину заміняється перевірочною
на m розрядів уліво (приписування наприкінці комбінації m нулів). Надалі додана частину заміняється перевірочною 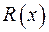 .
.
Перевірочна частина утворюється як залишок від ділення в кінцевому полі добутку 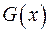 ∙ хm на поліном
∙ хm на поліном 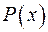 :
:
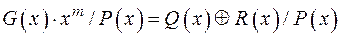 , (3)
, (3)
де 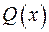 – ціла частка від ділення;
– ціла частка від ділення;
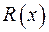 – залишок, що містить
– залишок, що містить  розрядів.
розрядів.
Після перемножування виразу (3) на 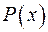 і перенесення
і перенесення 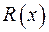 в іншу частину рівності без зміни знака, одержимо:
в іншу частину рівності без зміни знака, одержимо:
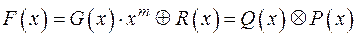 , (4)
, (4)
де 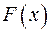 – циклічний код, утворений для кодової комбінації
– циклічний код, утворений для кодової комбінації 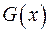 .
.
З виразу (4) маємо, що циклічний код математично може бути отриманий двома способами:
а) як результат додавання добутку 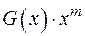 із залишком
із залишком 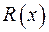 ;
;
б) як результат перемножування частки 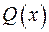 на утворюючий поліном
на утворюючий поліном 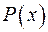 .
.
Приклад. Одержати циклічний код для інформаційного коду 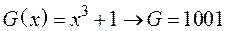 й утворюючого полінома
й утворюючого полінома 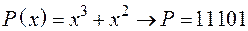 .
.
1 Знаходимо добуток 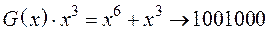 .
.
2 Проводимо ділення 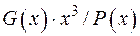 :
:

3 Визначаємо комбінацію циклічного коду:
а) як результат додавання добутку 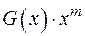 із залишком
із залишком 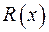 :
:
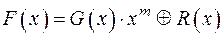 ;
;
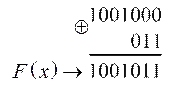
б) як результат перемножування частки 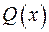 на утворюючий поліном
на утворюючий поліном 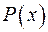 :
:
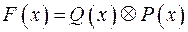 ;
;
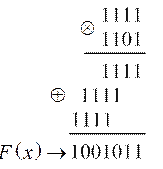
 2017-11-01
2017-11-01 1166
1166








