2017-11-01
352
Графическая интерпретация полученных результатов позволяет сделать вывод, что размеры деталей группируются около некоторой центральной величины (центра группирования), причем, чем больше отличие между этой величиной и выделенным интервалом, тем меньше частота регистрации размеров в данном интервале. Эта центральная величина называется средним арифметическим значением случайных величин и определяется по следующим формулам
; 
; 
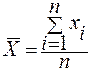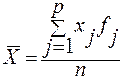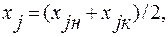(13.11)
где,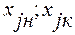 
- конечное и начальное значение случайной величины в интервале под номером 
, 
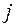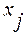- значение случайной величины в середине этого интервала, 
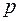- количество интервалов.
Другой характеристикой кривой распределения случайных величин, является среднее квадратическое отклонение этихвеличин от среднего арифметического значения, которое определяется по формулам
; 
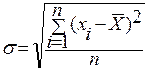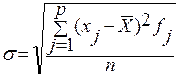. (13.12)
Среднее квадратическое отклонение является мерой рассеивания случайных величин. Среднее арифметическое значение и среднее квадратическое отклонение называются статистическими параметрами эмпирической кривой распределения.
|
|
|
