2017-11-01
1145
Введем новую переменную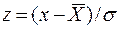 
. После замены переменной в (13.13) для плотности вероятности
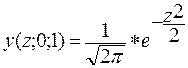(13.19)
Соответственно для интеграла вероятности (13.14) будем иметь
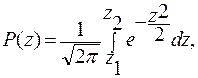(13.20)
где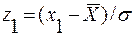 
и 
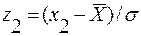- новые пределы интегрирования.
Это действие называется нормированием распределения случайных величин.
Сущность операции нормирования заключается к приведению множества кривых распределения к одной, зависящей только от нормированной переменной. Для этой кривой среднее арифметическое значение равно нулю, а среднее квадратическое отклонение равно единице. Графическая интерпретация процедуры нормирования заключается в совмещении центра группирования с началом новой системы координат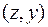 
(рис. 13.5). В этом случае кривая нормированного нормального распределения становится симметричной относительно оси ординат, а функция 
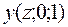называется плотностью нормированного распределения.
Функция Лапласа
Применение функции Лапласа позволяет вычислить теоретические частость и частоту. Примем в формуле (13.20)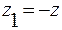 
; 
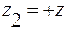. Тогда 
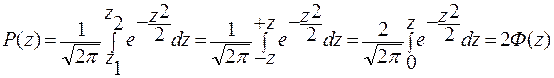. (13.21)
|
|
|
Интеграл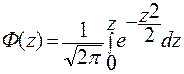 
называется функцией Лапласа.
Геометрически функцией Лапласа определяется площадь фигуры под кривой нормированного нормального распределения в промежутке от 0 до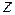 
. Интеграл в 
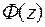нельзя выразить в элементарных функциях и его значение задано в специальных таблицах.
Выразим теоретическую частость через функции Лапласа. Выполним операцию нормирования. В результате замены переменной в формуле (13.13) будем иметь
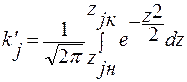. (13.22)
Пусть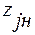 
< 
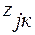. Тогда, выражая 
через функции Лапласа, получим
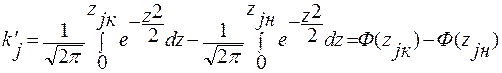, (13.23)
где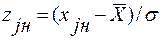 
и 
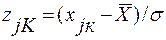- новые пределы интегрирования.
Тогда
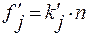(13.24)
