2017-11-01
373
В математической статистике доказано и подтверждено многочисленными экспериментами, что для многих случайных процессов теоретическая частость подчиняется закону нормального распределения и определяется следующим выражением
. (13.13)
В нем функция
называется плотностью вероятности непрерывной случайной величины или дифференциальной функцией нормального распределения. График этой функции в виде холмообразной кривой приведен на рис. 13.2. Этот график называется дифференциальной кривой нормального распределения или просто кривой нормального распределения. Запись 
означает, что плотность вероятности является функцией от непрерывной случайной величины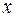 
и двух параметров распределения: 
- среднего арифметического значения и 
- среднего квадратического отклонения. Плотность вероятности следует рассматривать, как вероятность появления случайной величины 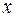на бесконечно малом отрезке в области ее определения, т.е. в точке. Там где 
, вероятность появления случайной величины максимальная. С увеличением разности 
эта вероятность уменьшается.
|
|
|
Чтобы определить саму вероятность появления случайной величины 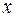в некотором интервале 
, необходимо вычислить интеграл от плотности вероятности
, 
. (13.14)
Это выражение называется интегральной функцией нормального распределения или интегралом вероятности. В геометрическом смысле этот интеграл представляет собой площадь под кривой нормального распределения в пределах заданного интервала. Для достаточно узкого интервала согласно теореме о среднем
; 
. (13.15)
Плотность вероятности имеет следующие свойства:
1. Ось 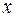является асимптотой для ветвей ее графика.
2. При 
плотность вероятности имеет максимальное значение
. (13.16)
3. График функции имеет две точки перегиба 
и 
, которые находятся на расстоянии 
от оси симметрии (рис.13.2). Ординаты их равны
. (13.17)
4. Если случайная величина может принимать любые численные значения в интервале 
, то независимо от 
и 
. (13.18)
Это свойство вытекает из положения, что вероятность появления случайной величины на бесконечно большом интервале равна единице.
Положение кривой относительно начала координат, и ее форма определяются двумя параметрами 
и . С изменением форма кривой остается прежней. Изменяется ее положение относительно начала координат (рис. 13.3). С изменением центр кривой остается на прежнем месте. Изменяется ее форма (рис.13.4). С увеличением кривая растягивается и уменьшается по высоте. Таким образом, как это уже было отмечено ранее, является мерой рассеяния случайной величины.
