Операция над случайными величинами

1) При умножении случайной величины х на число k отличное от 0, получается случайная величина k*х со значениями kxi с теми же вероятностями.

Хi

Xi
pi	0,1	0,4	0,5

 

kX

kX1	K	2K	3K
pi	0,1	0,4	0,5

2) При возведении в степень случайной величины Х в степень k получаем случайную величину 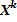со значениями 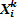и с теми же самыми вероятностями.

3) Сложением, вычитанием и умножением двух случайных величин получаются случайные величины со значениями хi ± yi, xi * yi с вероятностями pi * pj = p [(X=xi) * (Y=yi)]

Хi

хi	-2	-1
pi	0,1	0,3	0,15	0,2	0,25

 

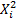
pi	0,1	0,3	0,15	0,2	0,25

 

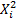
pi	0,15	0,5	0,35

Функция распределения. Свойства функции распределения.

Функцией распределения случайной величины называется функция F(X), которая показывает вероятность того, что случайная величина Х-большая примет значение меньше х-малое.

Для дискретной случайной величины функция распределения представляет собой ступеньчетую функцию.

Пример

Хi
Pi	0,4	0,1	0,3	0,2

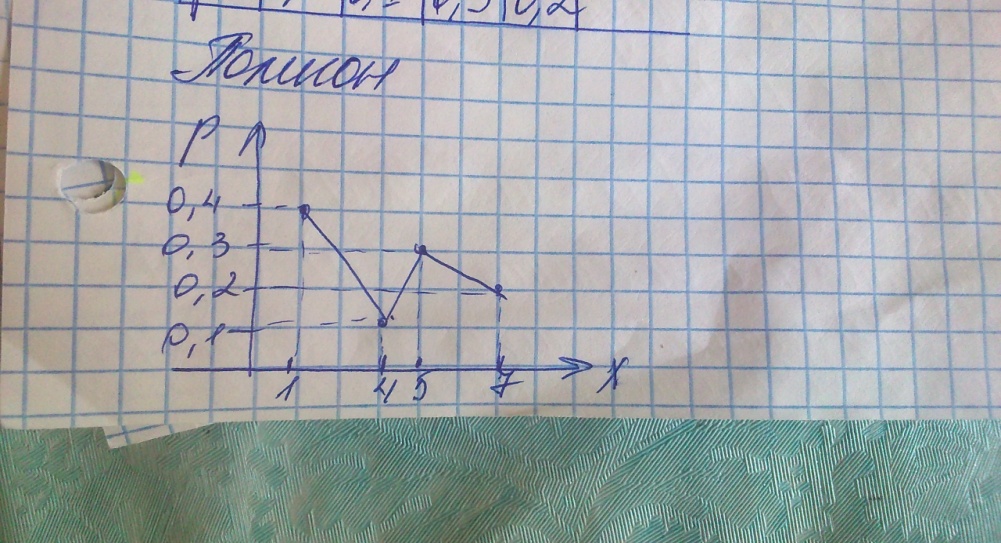
М(Х) = 1*0,4 +4 *0,1 +5 * 0,3 + 7*0,2 =3,7

Д(Х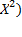) = М( - (М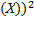

М(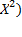 =1 *0,4 +16*0,1+2,5*0,3+4,9*0,2=19,3

Д(Х) = 19,3 – 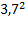= 5,61

Свойства функции распределения.

1) Функция F(X) монотонно не убывающая функция.

2) 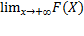=1,

0 ≤ F(X) ≤ 1

3) P(a ˂ X ≤ b) = F (b) –F (a)

14.Плотность вероятности и ее свойства.

Плотностью вероятности назыв. Ф-я f(x), являющаяся производной от ф-ии распределения. f(x)=F’(X).

Св-ва плотности вероятности: