Дискретной назыв. СВ, которая принимает отдельное значение в соответствующими им вероятностями.
Математическим ожиданием ДСВ называют сумму произведений всех ее возможных значений на их вероятности:
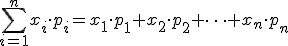
Свойства математического ожидания:
1. Математическое ожидание постоянной величины равно самой постоянной:
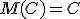
2. Постоянный можно выносить за знак математического ожидания:
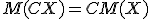
3. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:
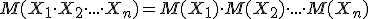
4. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:
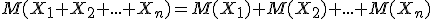
(для разности аналогично)
Дисперсией случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
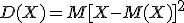
Дисперсию удобно вычислять по формуле:
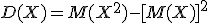
Свойства дисперсии:
1. Дисперсия постоянной равна нулю:
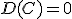
2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:
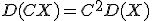
3. Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых:
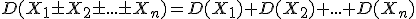
4. 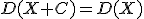
Средним квадратическим отклонением СВ называют квадратный корень из дисперсии:
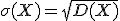
Модой называется наиболее вероятное значение СВ. Mo(X).
Рассмотрим следующие задачи.
1. Математическое ожидание и дисперсия СВ Х соответственно равны 0,5 и 5. Найти математическое ожидание и дисперсию случайной величины 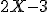 .
.
Решение.
Согласно свойствам математического ожидания и дисперсии, получаем:
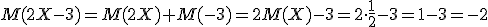
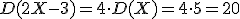
2. Случайные величины X и Y независимы, причем 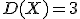 и
и 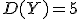 . Найти
. Найти 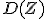 , если
, если 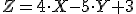 .
.
Решение.
На основании свойств дисперсии получаем:
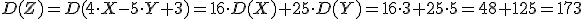
 2017-11-01
2017-11-01 1793
1793
