2017-11-01
1129
Если n неограниченно возрастает, а р бесконечно мало и не равно 0 и 1, то вероятность того, что в n независимых испытаниях событие А произойдет не менее А раз, но не более В раз вычисляется по формуле:
Р (а ≤ m ≤ b) = Ф (Х2) – Ф (Х1) (формула А)
Если тут 2,то формулу А делим на 
Ф(х) =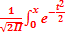 
dt
1. Функция Ф(х) нечетная.
2. Функция Ф(х) монотонно неубывающая
, 
.
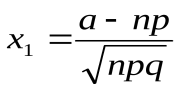Задача: Найти вероятность того, что из 1800 банков имеют уставной фонд свыше 100 000 000 от 300 до 400 банков включительно.
а = 300
в = 400
Р (300 ≤ m ≤ 400) = Ф (2,36) – Ф (-3,57) = Ф (2,36) + Ф (3,57) = 0,4909 + 0,499841 = 0, 990741
Х1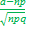 
= 
= 
= 
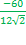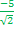= -3,57
Х2 = 
= 
= 
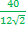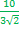= 2,36
Задача: Строительная фирма занимающаяся строительством коттеджей раскладывает рекламные листки по ящикам. Прежний опыт работы показывает, что примерно в одном случае из двух тысяч следует заказ. Найти вероятность того, что при размещении 100 000 листовок число заказов будет:
А) равно 48
Б)находится в границах от 45 до 55.
Решение:
а) n = 100 000
m = 40
p = 
q = 
λ = n * p = 50 ˃10
x =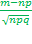 
= 
= - 0,28
f = (-0,28) = 0,3836
P100 000 (48) =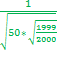 
* 0,3836 = 
= 0,0054
Б) n = 100 000
|
|
|
45≤ m≤ 55
p =
q =
P(45≤m≤55) = Ф (0,707) – Ф (-0,707) = Ф (0,707) + Ф (0,707) = 2Ф (0,707)= 2* 0,4564 =0,9128
Х1 = 
= 
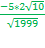= 0,707
Х2 = 
= 0,707
Рассмотрим следствие интегральной теоремы МуавраЛапласа.
Следствие. Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то при достаточно большом числе n независимых испытаний вероятность того, что:
а) число m наступлений события А отличается от произведения nр не более, чем на величину ε > 0 (по абсолютной величине), т.е.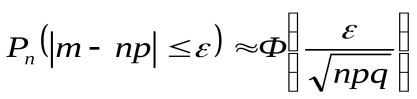 
;
б) частость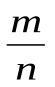 
события А заключена в пределах от α до β (включительно), т.е. 
, Где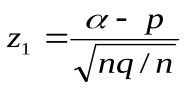 
, 
.
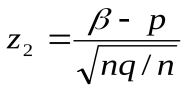в) частость 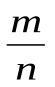события А отличается от его вероятности р не более, чем на величину Δ > 0 (по абсолютной величине), т.е. 
.
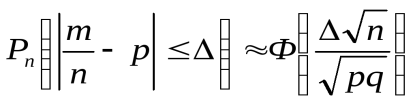□ 1) Неравенство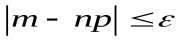 
равносильно двойному неравенству пр - Е ~ т ~ пр + Е. Поэтому по интегральной формуле 
:
.
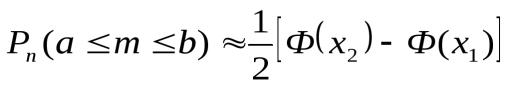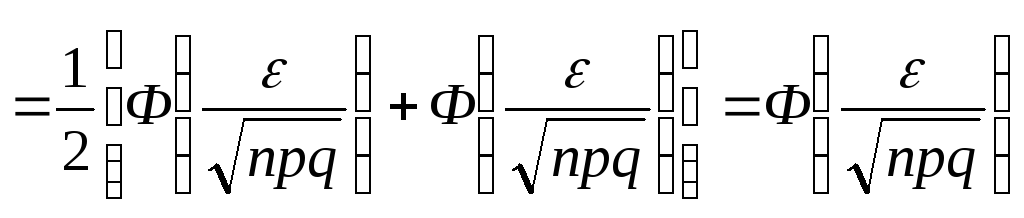2) Неравенство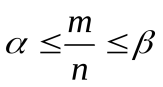 
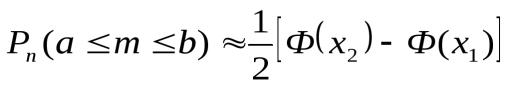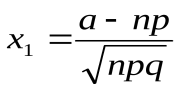равносильно неравенствуa ≤ m ≤ b при a = nα и b = nβ. Заменяя в формулах и , величины а иb полученными выражениями, получим доказываемые формулы и , .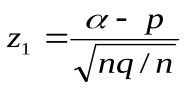
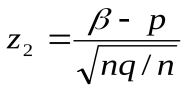3) Неравенство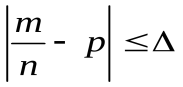 
равносильно неравенству 
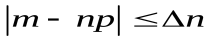. Заменяя в формуле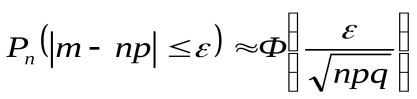 
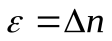, получим доказываемую формулу .
Пример. По статистическим данным в среднем 87% новорожденных доживают до 50 лет. Найти вероятность того, что из 1000 новорожденных доля (частость) доживших до 50 лет будет: а) заключена в пределах от 0,9 до 0,95; б) будет отличаться от вероятности этого события не более, чем на 0,04 (по абсолютной величине)?
Решение. а) Вероятность р того, что новорожденный доживет до 50 лет, равна 0,87. Т.к. n = 1000 велико (условие npq = 1000·0,87·0,13 = 113,1 ≥ 20 выполнено), то используем следствие интегральной теоремы Муавра-Лапласа. Вначале определим:
, 
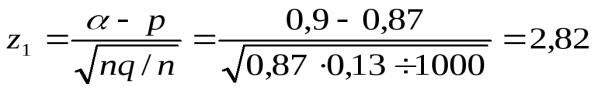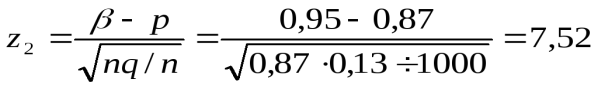. Теперь по формуле 
:
|
|
|
.
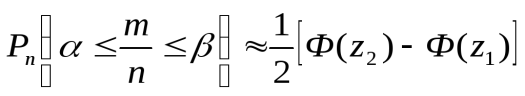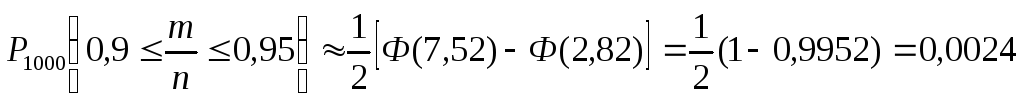Б) По формуле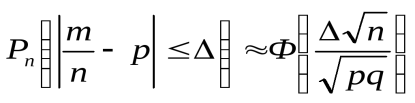 
:
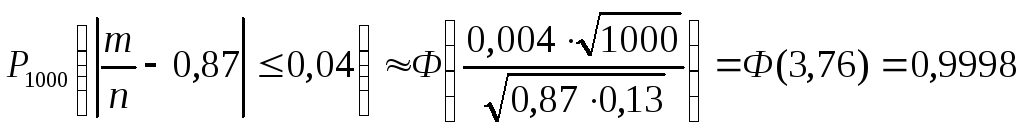. Так как неравенство 
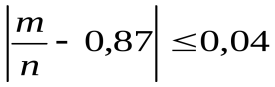равносильно неравенству 
, полученный результат означает, что практически достоверно, что от 0,83 до 0,91 числа новорожденных из 1000 доживут до 50 лет.
