ОПРЕДЕЛЕНИЯ АБСЦИССЫ ПАДЕНИЯ ШАРООБРАЗНЫХ
ЧАСТИЦ С НАКЛОННОЙ ПОЛКИ
Целью работы является определение математического ожидания абсциссы падения частиц шарообразной формы с наклонной полки в неподвижной среде и расчет основных характеристик кривой распределения.
Основы теории
Для характеристики частоты появления различных значений случайной величины x (в нашем случае погрешности определения абсциссы падения частиц) в теории вероятности применяют различные законы распределения случайной величины, причем во всех случаях кривая плотности распределения вероятностей определяется соотношением
 . 3.1)
. 3.1)
Наиболее часто используемым в теории вероятностей законом распределения является нормальный закон (распределение Гаусса), плотность вероятности которого описывается выражением
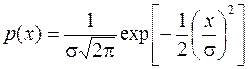 (3.2)
(3.2)
Координата центра распределения может характеризоваться несколькими величинами:
· медиана – такая точка на оси абсцисс, слева и справа, от которой вероятности появления различных значений случайной величины равны друг другу и составляют 50 %;
· мода – только для симметричных распределений точка на оси абсцисс, имеющая максимальную плотность распределения.
· математическое ожидание – центр тяжести распределения, то есть такая точка на оси абсцисс, относительно которой опрокидывающий момент равен нулю, или
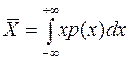 . (3.3)
. (3.3)
В нашем случае для дискретного распределения
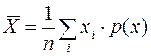 , (3.4)
, (3.4)
где n – количество частиц;
p(x) – количество частиц, попавших в i - ю ячейку;
x i – расстояние до середины i - й ячейки.
Если из всех наблюдавшихся значений погрешности вычесть систематическую составляющую, то есть перенести начало координат в центр распределения, то такое распределение называется центрированным.
Для описания различных свойств распределений используют такие параметры как моменты, причем первый центральный момент называется математическим ожиданием.
Центральный момент k -го порядка для случайной дискретной величины выражается как  . (3.5)
. (3.5)
Второй центральный момент называется дисперсией случайной величины
 . (3.6)
. (3.6)
Для более наглядной характеристики самого рассеяния пользуются корнем квадратным из дисперсии – средне квадратичным отклонением (СКО)
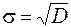 . (3.7)
. (3.7)
Третий центральный момент характеризует асимметрию, то есть скошенность распределения: когда один спад – крутой, а другой – пологий. Для относительной характеристики асимметрии используют безразмерный коэффициент асимметрии
 . (3.8)
. (3.8)
Четвертый центральный момент характеризует протяженность распределения, его относительное значение называют эксцессом.
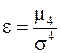 (3.9)
(3.9)
Не нужно путать его с коэффициентом эксцесса, равным
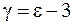 . (3.10)
. (3.10)
Для классификации распределений по их форме удобнее использовать другую функцию – контрэксцесс
 . (3.11)
. (3.11)
Одним из условий правомерности статистической обработки выборки является требование ее однородности. Отсчеты, резко отклоняющиеся по своим значениям от большинства других отсчетов, принято называть промахами и исключать из выборки. Наиболее предпочтительной является методика исключения промахов, предложенная Г.А. Агекяном [1], который рекомендует оценки 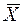 и s определять без использования отсчетов, предполагаемых промахами, а границу цензуирования назначать в зависимости от объема выборки n:
и s определять без использования отсчетов, предполагаемых промахами, а границу цензуирования назначать в зависимости от объема выборки n:
при 6 < n £ 100 | X гр| = 4s; (3.12)
при 100 < n £ 1000 | X гр| = 4,5s; (3.13)
при 1000 < n £ 10000 | X гр| = 5s. (3.14)
Если промахи попадают в этот интервал, их включают в расчет оценки 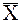 и s и все заново пересчитывают.
и s и все заново пересчитывают.
Для определения формы распределения, медианы и других характеристик выборка должна быть представлена в виде гистограммы, состоящей из m столбцов с определенной протяженностью d соответствующих им интервалов. При большом m гистограмма будет отличаться от плавной кривой распределения вследствие изрезанности многими всплесками и провалами. При слишком малом m гистограмма будет отличаться от действительной кривой распределения вследствие слишком крупной ступенчатости, из-за чего характерные особенности будут просто потеряны.
При объеме выборки, равном n, и величине контр эксцесса c наиболее предпочтительной для определения количества интервалов, является формула И.У. Алексеевой [2]
 . (3.15)
. (3.15)
Значение m принято выбирать нечетным, для того чтобы не искажалась середина кривой распределения.
 2017-11-01
2017-11-01 282
282








