Будущая стоимость денежной единицы

Время, как фактор в финансовых и коммерческих расчетах

Приведение вперед и назад по оси времени

В практических финансовых и коммерческих операциях суммы денег обязательно связываются с некоторыми конкретными моментами или интервалами времени. Для этого в контрактах фиксируются соответствующие сроки, даты, периодичность поступлений денежных средств или их выплат.

Фактор времени играет не меньшую роль, чем размеры денежных сумм. Необходимость учета фактора времени определяется принципом неравноценности денег, относящихся к разным моментам времени. Дело в том, что даже в условиях отсутствия инфляции и риска 1 млн.руб., полученный через год, не равноценен этой же сумме, поступившей сегодня.

Неравноценность определяется тем, что теоретически любая сумма денег может быть инвестирована и принести доход. Поступившие доходы в свою очередь могут быть реинвестированы и т.д. Следовательно, сегодняшние деньги в этом смысле ценнее будущих, а будущие поступления менее ценны, чем деньги текущего дня.

В финансовых вычислениях фактор времени обязательно учитывается в качестве одного из важнейших элементов. Его учет осуществляется с помощью начисления процентов[8].

Временная оценка денежных потоков основана на использовании шести функций сложного процента, или шести функций денежной единицы:

(накопленная (наращенная) сумма единицы).

Вычисление наращенной суммы на основе сложных процентов означает, что начисленные на первоначальную сумму проценты присоединяются к ней, а начисление процентов в последующих периодах производится на уже наращенную сумму.

Механизм наращения первоначальной суммы (капитала) по сложным процентам называют капитализацией.

Расчет наращенной суммы по сложным процентам производится по формуле:

FV = PV × (1 + i),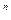

где FV – наращенная сумма; PV – текущая (первоначальная) сумма, на которую начисляется процент; i – годовая ставка сложных процентов, выраженная десятичной дробью; n –число лет, в течение которых начисляют проценты.

Начисление процентов может производится чаще, чем один раз в год (по полугодиям, кварталам, помесячно, ежедневно). Тогда для вычисления наращенной суммы используют формулу:

FV = PV × (1 + ),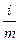

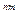где FV – наращенная сумма; PV – текущая (первоначальная) сумма, на которую начисляется процент; i – годовая ставка сложных процентов, выраженная десятичной дробью; n –число лет, в течение которых начисляют проценты; m – число периодов начисления процентов в году.

Годовая ставка начисления процентов i – называется номинальной. Кроме номинальной ставки существует понятие эффективной (действительной) процентной ставки которая измеряет относительный доход в целом за год при многоразовом начислении процентов по ставке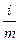. Эффективная ставка сложных процентов определяется по формуле:

i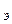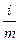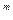= (1 + )– 1

Например. Депозит в размере 500 рублей внесен в банк на 3 года под 10% годовых. Нужно определить:

– наращенную сумму:

а) если начисление процентов производится один раз в году;

б) если начисление процентов производится ежеквартально;

в) если начисление процентов производится ежемесячно.

– эффективную ставку сложных процентов при ежеквартальном начислении процентов.

Решение:

FV = PV × (1 + i)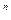= 500 × (1 + 0,10)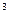= 666 руб.

FV = PV × (1 + 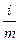)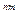= 500 × (1 +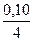)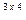= 672 руб.

FV = PV × (1 + 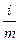)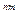= 500 × (1 +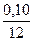)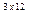= 674 руб.

i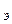= (1 + 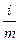)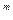– 1= (1 + 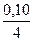)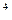– 1 = 0,1038 (10,38 %)