Задача составления оптимального портфеля для осторожного инвестора.
Задача составления оптимального портфеля для рискового инвестора.
Как отмечалось ранее, что такой инвестор готов идти на некоторый фиксированный уровень риска V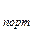 , добиваясь при этом максимальной эффективности. Математически это приводит к следующей задаче нелинейного программирования:
, добиваясь при этом максимальной эффективности. Математически это приводит к следующей задаче нелинейного программирования:
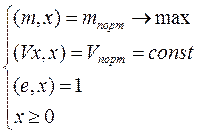
Если в этой задаче опустить условие не отрицательности (x ³0), то задача допускает точное решение. При этом некоторые x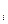 могут быть отрицательными. Соответствующие ценные бумаги должны быть взяты в долг. Решение этой задачи и анализ дан в главе 6. С условием не отрицательности задача численно проанализирована в главе 10.
могут быть отрицательными. Соответствующие ценные бумаги должны быть взяты в долг. Решение этой задачи и анализ дан в главе 6. С условием не отрицательности задача численно проанализирована в главе 10.
Осторожный инвестор готов ограничиться заранее заданной эффективностью портфеля 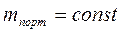 , но при этом добивается минимального риска:
, но при этом добивается минимального риска:
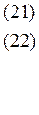
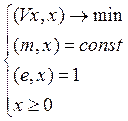
Так как целевая функция (7) является квадратичной, а ограничения линейны, то получим задачу квадратичного программирования, которая решается симплекс-методом. Впервые задачу составления оптимального портфеля ценных бумаг именно в таком виде поставил Г.Марковиц в 1952г в статье с названием «Выбор портфеля», и которая стала началом нового этапа развития финансовой математики.
Для того, чтобы составить согласованные портфели ценных бумаг необходимо критерии (15) и (16) объединить в один критерий, то есть задачу векторной оптимизации преобразовать в задачу нелинейного программирования. Рассмотрим два различных способа, а именно мультипликативный и аддитивный способы преобразования.
Мультипликативное сворачивание может быть определено по-разному и приводит в простейшем случае к следующей задаче нелинейного программирования:
|
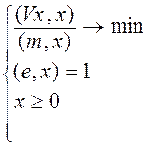
Аддитивное сворачивание приводит в общем случае к следующей задаче квадратичного программирования:
|
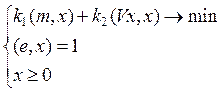
Здесь коэффициенты k1(k1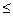 0) и k2(k2>0) характеризуют отношение инвестора к риску и доходности. Очевидно, что решение этой задачи зависит, на самом деле, от коэффициента относительного предпочтения k=k
0) и k2(k2>0) характеризуют отношение инвестора к риску и доходности. Очевидно, что решение этой задачи зависит, на самом деле, от коэффициента относительного предпочтения k=k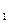 /k
/k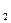 и целевая функция в задаче (10) может быть записана в виде:
и целевая функция в задаче (10) может быть записана в виде:
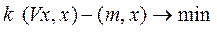
Впервые эта функция полезности введена в рассмотрение М.Рубинштейном [5].
 2014-01-28
2014-01-28 701
701








