Теорема об обобщенных множителях Лагранжа

Пусть x^* - решение основной задачи нелинейного программирования и

1. функции 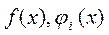, i=1,…,m – дифференцируемые в Eⁿ,

2. градиенты активных в этой точке ограничений 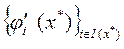- линейно независимы,

тогда существуют числа 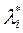, , 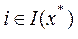называемые обобщенными множителями Лагранжа, что выполняются утверждения:

1⁰. 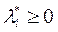, iÎI(x)

(36)

2⁰.

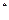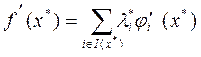
Замечание 1. Необходимое условие для общей задачи нелинейного программирования (30)-(32) получается простым объединением приведенных выше теорем и поэтому здесь опускается.

Замечание 2. Для удобства использования теорем о множителях Лагранжа обычно вводят функцию Лагранжа

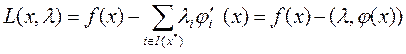
Положим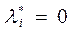,если 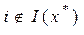и тогда (34) или (36) примут вид:

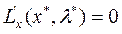
Докажем одно вспомогательное неравенство, важное для решения задачи составления оптимального портфеля.

(37)

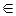
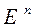Лемма 1. Для любой симметричной и положительно определенной матрицы и любых векторов x, y справедливо неравенство:

,

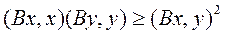причем равенство возникает лишь при

y=kx,

где k – некоторое число.

Доказательство.