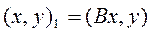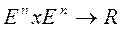Введем в рассмотрение функцию

: .

Так как, B – симметричная и положительно определенная матрица, то непосредственной проверкой показывается, что эта функция является скалярным произведением. Обозначим

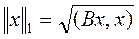
норму, порожденную этим скалярным произведением.

Применяя к введенному скалярному произведению, неравенство Коши-Буняковского получаем:

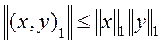
Возводя обе части в квадрат, получаем неравенство (37).

Лемма доказана.

Лемма 2. Пусть V –симметричная, положительно определенная матрица, m 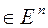- произвольный вектор,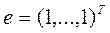, тогда

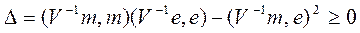причем 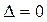тогда и только тогда, когда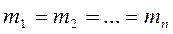

Доказательство.

Положив 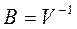и x=m, y=e получаем, что неравенство (38) эквивалентна неравенству (37), причем оно обращается в ноль лишь при m=ke, где k – некоторое число, но тогда

.

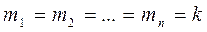Лемма доказана.