МАТЕМАТИЧЕСКИОЕ ОПИСАНИЕ МЕТОДОВ СПЕКТРАЛЬНОГО РАЗЛОЖЕНИЯ СИГНАЛОВ
Бесконечная система действительных ненулевых функций
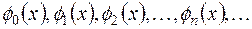 (2.1)
(2.1)
называется ортогональной на отрезке [a,b], если
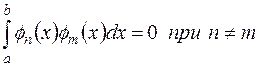 (2.2)
(2.2)
Это условие (2.2) выражает попарную ортогональность функций системы (2.1).
Интервал [a,b] называется интервалом ортогональности системы функций.
Величина
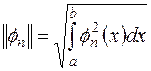 (2.3)
(2.3)
называется нормой функции 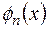 .
.
Функция 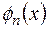 , для которой выполняется условие
, для которой выполняется условие
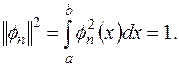 (2.4)
(2.4)
называется нормированной функцией, а система нормированных функций (2.1), для двух функций которой выполняется условие ортогональности (2.2), называется ортонормированной системой.
Доказано, что если функции 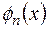 , то произвольная кусочно-непрерывная функция
, то произвольная кусочно-непрерывная функция 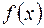 , для которой выполняется условие:
, для которой выполняется условие:
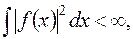 (2.5)
(2.5)
может быть представлена в виде суммы ряда
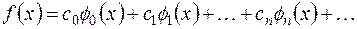 (2.6)
(2.6)
Коэффициенты ряда (2.6) определяются по формуле:
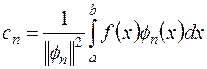 (2.7)
(2.7)
Таким образом, ряд (2.6), в котором коэффициенты 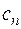 определяются по (2.7), называется обобщённым рядом Фурье по данной системе
определяются по (2.7), называется обобщённым рядом Фурье по данной системе 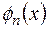 . Совокупность коэффициентов
. Совокупность коэффициентов 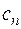 называется спектром сигнала в данной ортогональной системе и полностью определяется этот сигнал.
называется спектром сигнала в данной ортогональной системе и полностью определяется этот сигнал.
Обобщённый ряд Фурье обладает следующим важным свойством: при заданной системе функций 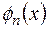 и фиксированном числе слагаемых ряда (2.6) он обеспечивает наилучшую аппроксимацию (в смысле минимума среднеквадратической ошибки) данной функции
и фиксированном числе слагаемых ряда (2.6) он обеспечивает наилучшую аппроксимацию (в смысле минимума среднеквадратической ошибки) данной функции 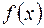 . Это означает, что среднеквадратическая ошибка, под которой подразумевается величина
. Это означает, что среднеквадратическая ошибка, под которой подразумевается величина
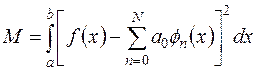 (2.8)
(2.8)
достигает минимума, когда коэффициенты ряда 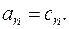
Из этого факта следует фундаментальное соотношение, справедливое для любой ортогональной системы, называемое неравенством Бесселя:
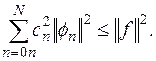 (2.9)
(2.9)
Ортогональная система называется полной, если увеличение числа членов ряда позволяет сделать среднеквадратическую ошибку М (2.8) сколь угодно малой. Условие полноты можно записать в виде соотношения:
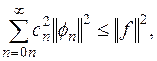 (2.10)
(2.10)
 |
называемого теоремой Парсеваля. При выполнении условия (2.10) можно считать, что ряд (2.6) сходится в среднем:
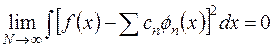 (2.11)
(2.11)
Из этого, однако, ещё не следует, что ряд сходится к 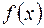 при любых значениях x.
при любых значениях x.
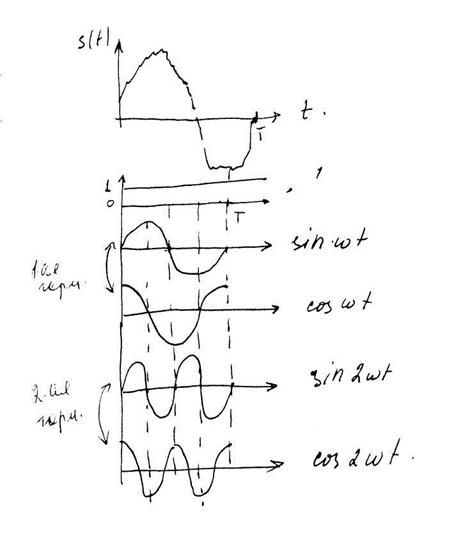
Основной практический интерес представлю полные ортонормированные системы функций, поскольку неполные системы не дают сходимости разложения для всех квадратично интегрируемых функций. Но, несмотря на это, некоторые неполные системы также находят применение. Например, выходное напряжение идеального фильтра нижних частот может быть точно представлено путём разложения в ряд по неполной ортогональной системе функций вида 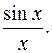
 2014-01-31
2014-01-31 1288
1288








