2014-01-31
4743
Квантование сигнала X(t) по уровню состоит в преобразовании непрерывного множества значений сигнала X(t) в дискретные. В результате квантования по уровню непрерывное множество значений сигнала X(t) в диапазоне от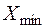 
до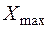 
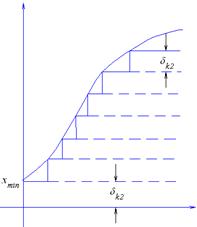
преобразуется в дискретное множество значений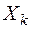 
- уровней квантования. В результате квантования по уровню образуется ступенчатая функция - 
.
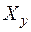Квантование по уровню широко используется в системах передачи информации, ИИС, при автоматическом управлении, контроле, обработке.
Шаг (интервал) квантования -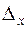 
- разность.
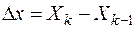
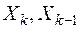- соседние уровни кантования.
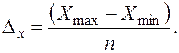
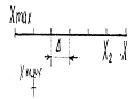
Квантование по уровню может быть равномерным и неравномерным. При равномерном квантовании по уровню – диапазон изменения сигнала X(t) разбивается на n одинаковых интервалов – интервалов квантования.
Квантование сигнала по уровню осуществляется с помощью нелинейного элемента – квантизатора.
Равномерное квантование преимущественно используется в технике, в связи с простотой техническое реализации.
Шкала Х значений сигнала x(t) может быть разбита на отдельные участки различным образом:
- с привязкой уровней квантования к x(t)=0,
- с привязкой уровней квантования к границам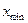 
и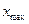 
диапазона изменения x(t).
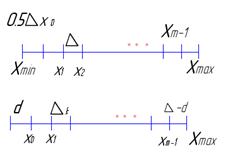Квантование по уровню практически осуществляется 2-мя способами:
1) Мгновенное значение функции x(t) заменяем меньшим дискретным значением.
2) Мгновенное значение функции заменяется ближайшим меньшим или большим дискретным значением в зависимости от того, какое значение к мгновенному значению функции. Переход со ступеньки на ступеньку при пересечении середины.
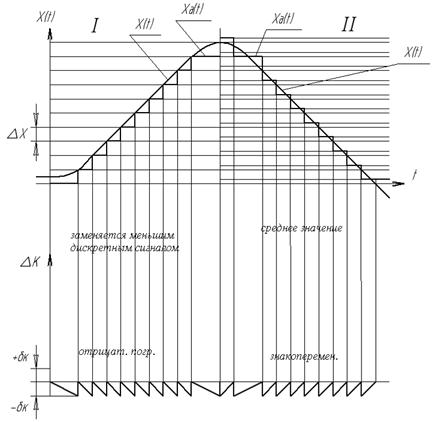
При квантовании по уровню появляются шумы или погрешности квантования (метод.), где каждое мгновенное значение заменяется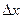 
-шаг (интервал) квантования – расстояние между соседними дискретными уровнями.
Погрешность квантования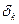 
связана с заменой истинного значения сигнала 
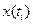некоторым уровнем квантования 
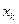, и 
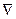- погрешность квантования по уровню, шумом квантования, является случайной величиной.
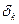- абсолютная погрешность квантования всегда отрицательная
;
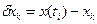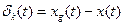
1.
      |    |
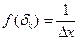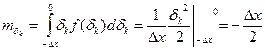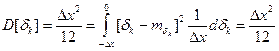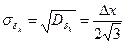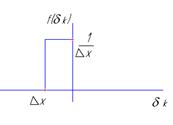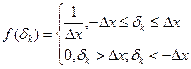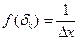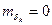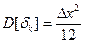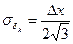Погрешность квантования при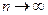 
подчиняется закону распределения равной вероятности.
;
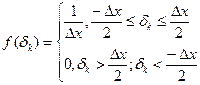
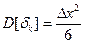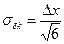повышается в 2 раза.
2.
;
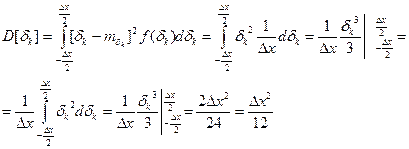
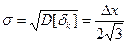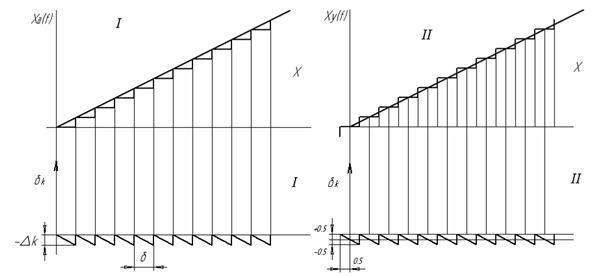
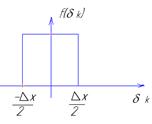
При 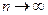погрешность квантования подчиняется закону распределения равной вероятности:
;
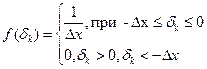
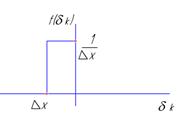Среднее значение (матем. ожидан.) погрешности квантования:
;
;
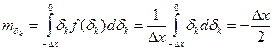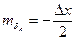Дисперсия погрешности квантования:
;
;
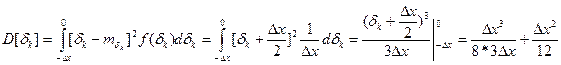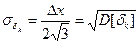2 способ:
При квантовании методом замены действительные мгновенные значения функции заменяются ближайшим меньшим или большим дискретным значением, погрешность квантования также подчиняется закону распределения равной вероятности, но изменяется в пределах от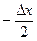 
до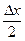 
.
;
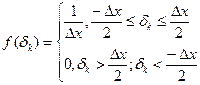
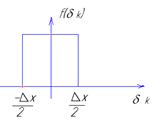Математическое ожидание (МО) погрешности квантования
(
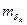) = 0.
Дисперсия погрешности:
;
;
;
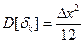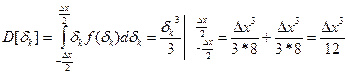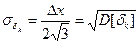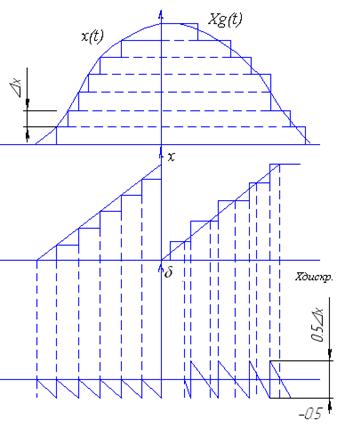
Одним из случаев квантования может быть квантование по уровню без фиксирования уровней относительно 0 (относительно нул. ур. х(t)). Квантование осуществляется путем замены значения x(t) ближайшим меньшим дискретным значением (уровнем). Нижний дискретный уровень принимается за первый. В этом случае среднеквадратичная погрешность квантования увеличивается в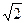 
раз.
;
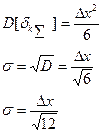Сигнал x(t) можно рассматривать как реализацию случайной величины Х с плотностью распределения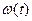 
. Можно найти характеристики случайной величины 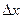погрешности квантования по уровню.
I)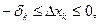 
II)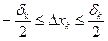 
;
Для k-го уровня квантования k=0,…,n-1. Математическое ожидание – погрешности квантования на:
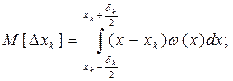
Дисперсия:
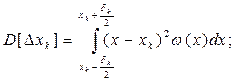
Примем:
Интервал квантования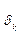 
мал по сравнению с диапазоном применения сигнала;
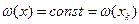
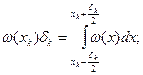
Тогда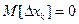 
.
Дисперсия погрешности квантования по уровню на интервале
.
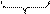
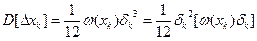Дисперсия равномерно вероятность попадания x(t) в
распределена интервале 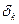квантования
в этом интервале сигнала
Дисперсия полной погрешности квантования по уровню для всего диапазона [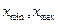
] можно получить суммирую выражение для 
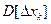по всем k уровням.
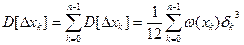
При равномерном шаге квантования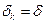 
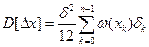
Есл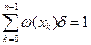и 
, при :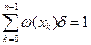 
;
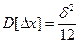Средне-квадратическая погрешность квантования сигнала по уровню для равномерного распределения:
;
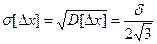Оптимальное квантование по уровню может быть обеспечено только неравномерным разбиением шкалы Х сигнала.
Лекция №15
