Во многих измерительных системах связи используется дискретное представление сигнала, т.е. непрерывный сигнал представляется своими дискретными значениями через промежуток времени 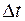 . Естественно ожидать, что такое представление может привести к потере информации. Но при определённом соотношении между шириной спектра сигнала и временным интервалом
. Естественно ожидать, что такое представление может привести к потере информации. Но при определённом соотношении между шириной спектра сигнала и временным интервалом 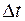 можно сохранить всю информацию, содержащуюся в сигнале. Это соотношение устанавливается теоремой отсчётов или теоремой Котельникова.
можно сохранить всю информацию, содержащуюся в сигнале. Это соотношение устанавливается теоремой отсчётов или теоремой Котельникова.
Владимир Александрович Котельников – академик, советский учёный в области радиотехники и радиофизики. 1933г. - теорема Котельникова.
Теорема Котельникова – если непрерывная функция X(t) удовлетворяет условиям Дирихле (ограничена, кусочно-непрерывная и имеет конечное число промежутков) и её спектр ограничен некоторой частотой 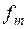 , то она полностью определяется последовательностью своих значений в точках, отстоящих друг от друга на расстоянии
, то она полностью определяется последовательностью своих значений в точках, отстоящих друг от друга на расстоянии 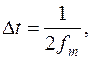 где
где 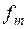 - максимальная частота спектра сигнала.
- максимальная частота спектра сигнала.
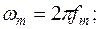
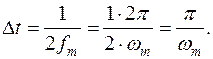
Условия Дирихле:
а) интервал, на котором функция определена, может быть разбит на конечное число интервалов, в каждом из которых 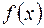 непрерывна и монотонна – функция ограничена;
непрерывна и монотонна – функция ограничена;
б) во всякой точке разрыва существуют значения 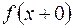 и
и 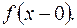
То есть при контроле прогресса, описываемого функцией 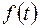 с ограниченным спектром, достаточно измерять мгновенные значения через промежутки времени
с ограниченным спектром, достаточно измерять мгновенные значения через промежутки времени 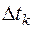 .
.
Выбор частоты отсчётов по теореме Котельникова.
1) Пусть сигнал, описываемый непрерывной функцией времени X(t), имеет ограниченный спектр, т.е. преобразование Фурье.
Спектральная функция 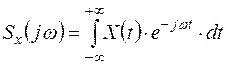 (прямое преобразование функции) удовлетворяет условию
(прямое преобразование функции) удовлетворяет условию 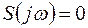 при
при 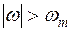 . X(t) удовлетворяет условию Дирихле
. X(t) удовлетворяет условию Дирихле 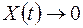 при
при 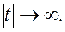
2) При представлении сигнала 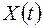 интегралом Фурье, пределы интегрирования можно ограничить значениями от
интегралом Фурье, пределы интегрирования можно ограничить значениями от 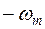 до
до 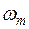 .
.
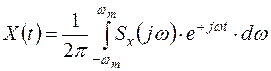 (обратное преобразование функции). Так как
(обратное преобразование функции). Так как 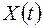 удовлетворяет условиям Дирихле, то и
удовлетворяет условиям Дирихле, то и 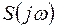 удовлетворяет условиям Дирихле. Считаем, что
удовлетворяет условиям Дирихле. Считаем, что 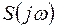 - функция частоты, её дополним до периодической, период которой равен
- функция частоты, её дополним до периодической, период которой равен 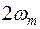 . Разложим эту функцию в ряд Фурье на интервале
. Разложим эту функцию в ряд Фурье на интервале 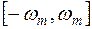 .
.
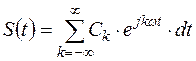 аналогично
аналогично 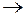
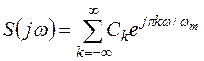 .
.
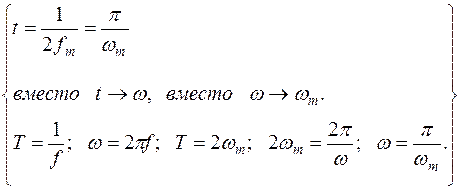
коэффициенты разложения
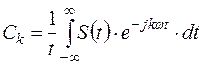 или
или 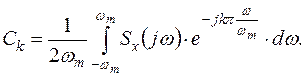
Сравниваем выражения для 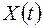 и
и 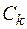 , видим, что они совпадают, если
, видим, что они совпадают, если 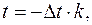 а это справедливо; а также
а это справедливо; а также 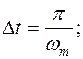
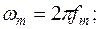
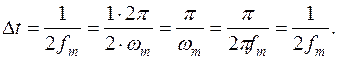
Отсюда 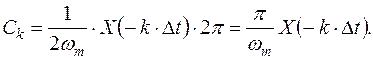
Подставляем выражение для 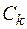 в
в 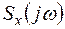 (ряд Фурье), получим спектральную функцию в виде:
(ряд Фурье), получим спектральную функцию в виде:
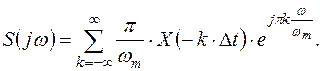
Подставив 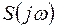 в X(t), т.е. перейдём к временной записи. Знак k изменим на противоположный с учётом того, что суммирование производится по всем отрицательным и положительным значениям k. Учитывая сходимость ряда и интеграла Фурье, изменим порядок операций интегрирования и
в X(t), т.е. перейдём к временной записи. Знак k изменим на противоположный с учётом того, что суммирование производится по всем отрицательным и положительным значениям k. Учитывая сходимость ряда и интеграла Фурье, изменим порядок операций интегрирования и  .
.
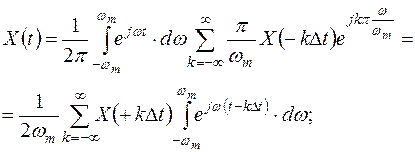
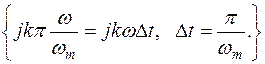
вычислим интеграл с учётом формулы Эйлера:
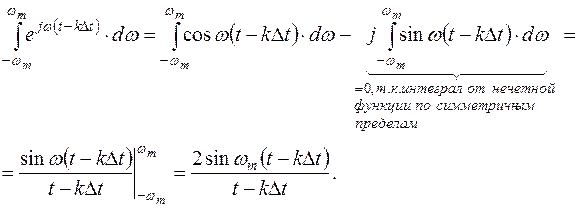
Тогда в окончательном виде X(t)
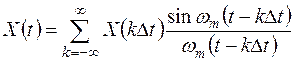 - ряд Котельникова.
- ряд Котельникова.
Это аналитическое выражение теоремы Котельникова, показывает, что непрерывная функция X(t) с ограниченным спектром может быть точно представлена отсчётами функции 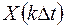 , взятыми через равные интервалы
, взятыми через равные интервалы 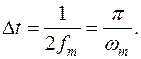
Лекция № 13
Непрерывная функция X(t) представляется суммой произведений, один из сомножителей – это коэффициент 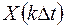 определяет значение функции в момент отсчёта, а другой – функция отсчётов.
определяет значение функции в момент отсчёта, а другой – функция отсчётов.

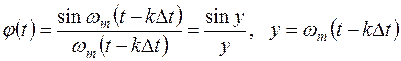 .
.
Функция имеет следующие свойства:
1) в момент времени 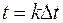 , функция
, функция 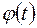 достигает наибольшего значения, т.е. равно 1.
достигает наибольшего значения, т.е. равно 1.
2) в момент времени, кратные 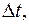 т.е.
т.е. 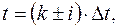 где i – любое целое число,
где i – любое целое число, 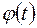 обращается в нуль.
обращается в нуль.
Теорема Котельникова относится к сигналам с ограниченным спектром.
Функция отсчётов – это реакция идеального фильтра нижних частот с граничной частотой 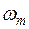 на
на 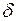 - функцию. Если через такой фильтр пропустить квантованный сигнал с
- функцию. Если через такой фильтр пропустить квантованный сигнал с 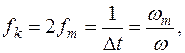 то сумма выходных сигналов фильтра даёт исходный непрерывный сигнал.
то сумма выходных сигналов фильтра даёт исходный непрерывный сигнал.
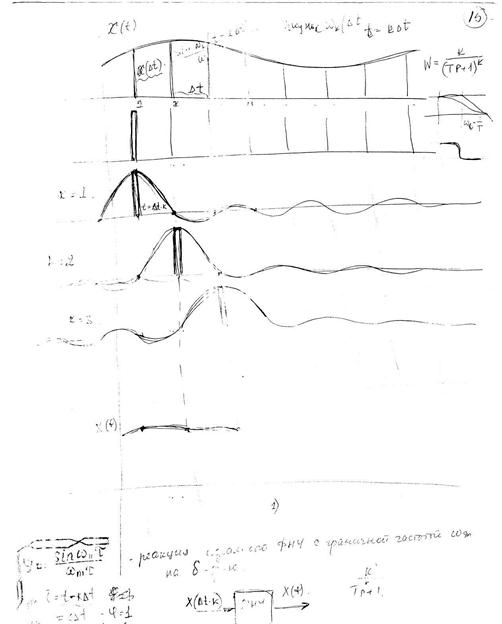
Поэтому с целью использования теоремы Котельникова для квантования сигналов, реальный спектр сигнала, простирается от 0 до 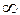 , условно ограничивают некоторый диапазон частот от 0 до
, условно ограничивают некоторый диапазон частот от 0 до 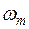 , в котором сосредоточена основная (подавляющая) часть энергии спектра.
, в котором сосредоточена основная (подавляющая) часть энергии спектра.
Практическое применение т. Котельникова встречает трудности:
1) реальные сигналы ограничены во времени и имеют бесконечный спектр, а это противоречит т. Котельникова.
2) для точного восстановления исходной функции необходимо получить и суммарные реакции фильтра на входные импульсы 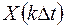 на всей оси времени от
на всей оси времени от 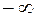 до
до 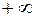 , или большого количества импульсов до и после аппр... участка функции. Это трудно практически реализовать. Функции отсчётов, генерируемые ФНЧ, должны иметь бесконечную протяжённость во времени, как для положительного t, так и для отрицательного t. Такие фильтры физически нереальны.
, или большого количества импульсов до и после аппр... участка функции. Это трудно практически реализовать. Функции отсчётов, генерируемые ФНЧ, должны иметь бесконечную протяжённость во времени, как для положительного t, так и для отрицательного t. Такие фильтры физически нереальны.
Если сигнал ограничен интервалом времени Т, то общее число отсчетов равно 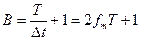 ,
, 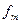 -частотная граница спектра сигнала. При 2
-частотная граница спектра сигнала. При 2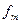 Т >> 1,
Т >> 1, 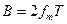 . Такой сигнал представляют конечной суммой или усеченным рядом Котельникова:
. Такой сигнал представляют конечной суммой или усеченным рядом Котельникова:
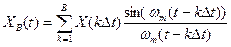
Число В  базой или числом степеней свободы сигнала. Относительная среде-кврадратичная погрешность, связанная с представлением сигнала Х(t) конечным числом отсчетов равна:
базой или числом степеней свободы сигнала. Относительная среде-кврадратичная погрешность, связанная с представлением сигнала Х(t) конечным числом отсчетов равна:
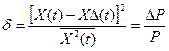 ,
,
где P – полная мощность (энегрия) сигнала, 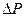 - энергия сосредоточенная вне полосы частот [-
- энергия сосредоточенная вне полосы частот [-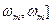 , характеризует погрешность, возникающую за счет ограничения спектра. Эта погрешность может быть определена как отношение:
, характеризует погрешность, возникающую за счет ограничения спектра. Эта погрешность может быть определена как отношение:
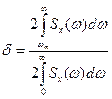 .
.
При заданной относительной погрешности квантования и известном энергетическом спектре процесса можно определить граничную частоту, а затем интервал квантования 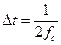 .
.
 2014-01-31
2014-01-31 1090
1090
