Для построения и анализа эконометрических моделей используются принципы выборочного метода. Суть метода состоит в том, что из полной совокупности объектов выбирают случайным образом n объектов. Данную выборку подвергают детальному исследованию, и по результатам делают вывод о всей совокупности (например, контроль качества партии товара по выбранным образцам).
Пусть эмпирические данные наблюдений { x1, x2, …, xn } представляют собой выборку значений случайной величины X, подчиняющейся нормальному распределению N (m,s 2), и по этим данным требуется оценить математическое ожидание (среднее значение) m= EX и дисперсию (среднеквадратичное отклонение от среднего значения) s 2=DX. Измеренные значения xi являются случайными величинами, причем Exi= m, Dxi= s 2. Интуиция подсказывает нам, что среднее арифметическое
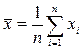
является лучшей оценкой для величины m, чем отдельные наблюдения xi. Действительно,
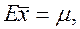
т.е. оценка является несмещенной, а дисперсия среднего
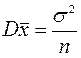
при n ®∞ стремится к нулю. Величину дисперсии s 2 можно оценить по данным xi известными формулами (см.4.5)
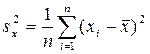
или
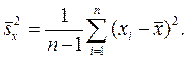 (8.1)
(8.1)
При этом известно [4], что оценка sx2 является смещенной оценкой
дисперсии s 2:
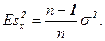
Оценка (8.1) несмещенная:
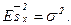
Для определения интервальной оценки неизвестного параметра m введем случайную величину
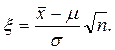 (8.2)
(8.2)
Можно доказать, что величина x распределена по нормальному закону с математическим ожиданием E x=0 и дисперсией D x=1, вследствие чего
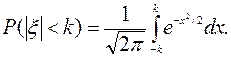
Полагая
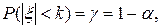
получим после элементарных преобразований, что с вероятностью g=1-a выполняется неравенство
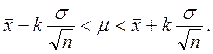 (8.3)
(8.3)
Вероятность того, что искомое значение параметра m не содержится в указанном интервале, равна a. Интервал
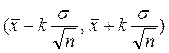
называется доверительным интервалом, отвечающим доверительной вероятности g.
Если, к примеру, k =2, доверительная вероятность g=0.955. Значению k =3 отвечает вероятность g = 0.997 (правило «трех сигм»).
Но для использования указанных доверительных интервалов на практике нужно знать стандартное отклонение s. Если значение s неизвестно, для
его оценки используется величина 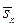 . В этом случае можно ввести случайную величину
. В этом случае можно ввести случайную величину
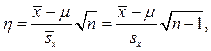
которая имеет распределение Стьюдента с n-1 степенью свободы [4]. Не выписывая здесь соответствующей функции распределения, приведем несколько значений доверительной вероятности g(k,n), отвечающих доверительному интервалу
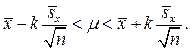 (8.4)
(8.4)
При k =2 и n =3 имеем g=0.817; при k =2 и n =7 вероятность g=0.908; g(3,3)=0.905; g(3,5)=0.96. С ростом n различие между распределением Стьюдента и нормальным распределением становится меньше, при n> 20 этим различием в большинстве случаев можно пренебречь.
В случае парной линейной регрессии y=a+bx мы предполагали, что для наблюдаемых значений (xi,yi), i = 1,2,....n выполняются равенства yi=a+bxi+ e i, где e i Î N (0, s2).
Можно доказать, что несмещенной оценкой для s 2 является число
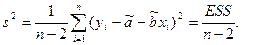 (8.5)
(8.5)
Величина s характеризует стандартное отклонение ошибок e i. В таблице из §5 её значение представлено в третьей строчке правого столбца. Что же касается стандартных отклонений для коэффициентов ã и b̃, то для их вычисления введем ковариационную матрицу Q= Covq, где
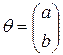
Элементы ковариационной матрицы
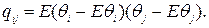
Можно доказать, что оценки ã и b̃ являются несмещенными, т.е. Eã=a, Eb̃=b.
Дисперсии Dã и Db̃ равны соответственно элементам q11 и q22 матрицы Q. Можно доказать, что ковариационная матрица вычисляется по формуле
Q= s 2 (XTX)-1.
В случае парной регрессии матрица (XTX) имеет вид (5.8).
Поэтому
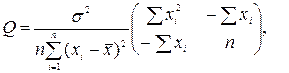
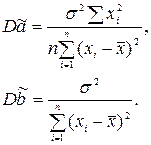
Подставляя вместо неизвестной дисперсии s 2 ее оценку (8.5) и извлекая квадратные корни, найдем оценки стандартных отклонений s a и sb коэффициентов регрессионного уравнения, которые содержатся во второй строчке таблицы из §5. Можно построить и доверительные интервалы для этих коэффициентов, если принять во внимание, что величины
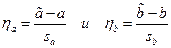
имеют распределение Стьюдента с n -2 степенями свободы.
Доверительный интервал для прогнозируемых значений величины y*=ã+b̃x*, отвечающей некоторому заданному значению x*, также определяется распределением Стьюдента. Его границы вычисляются по формуле
y = y* ± t (n- 2, 1- a/2)s * (8.6)
где коэффициент t (n- 2, 1 - a / 2) имеет тот же смысл, что и коэффициент k в формуле (8.4);
1-a — доверительная вероятность, равная, например, 0.95, в этом случае a =0.05;
n- 2 — число степеней свободы;
s* — стандартное отклонение случайного значения y*, которое можно вычислить по формуле
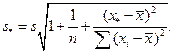
В пакете Statistica границы (8.6) вычисляются и изображаются на графиках регрессии (рис. 6).
Аналогично рассматривается общий случай множественной линейной регрессии y =Xq + e.
Можно показать, что дисперсия прогноза Dy*= s 2 [ x*T (XTX) -1x*+ 1], где x*= (x1*, x2*,…,xm*) T — заданный набор независимых переменных.
Несмещенной оценкой для s 2 является число
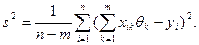
Поэтому оценка среднеквадратичного отклонения y* будет
sy* = s [(x*) T (XT X)- 1 x* + 1]1/2,
а граница доверительного интервала
y = y* ± sy*t (n-m, 1 - a / 2).
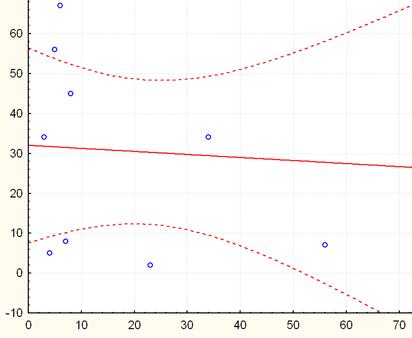
Рис.6. Изображение доверительного интервала в Statistica.
 2014-02-01
2014-02-01 755
755








