Временной ряд как случайный процесс

Пусть значение экономического показателя x (t) в любой момент времени t представляет собой случайную величину X (t). Предположим, что случайная величина X (t) является непрерывной. Тогда существует плотность вероятности p (x,t), по которой определяется вероятность случайного события

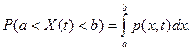
Рассмотрим также математическое ожидание

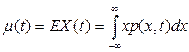(11.1)

и дисперсию

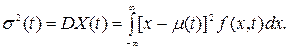(11.2)

Если плотность вероятности p (x,t) =p (x) не зависит от времени, то математическое ожидание и дисперсия будут постоянными величинами.

Рассмотрим два произвольных момента времени t₁ и t₂. Случайные величины X (t ₁) и X (t ₂) харатеризуются плотностью совместного распределения вероятностей p (x ₁ ,t ₁; x ₂ ,t ₂). При этом ковариация cov(X (t ₁) ,X (t ₂)) вычисляется по формуле

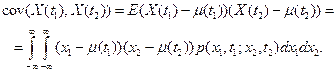
Аналогично рассматривается значение случайного процесса X (t) в трех, четырех и более точках t_k, при этом вводится многомерная плотность распределения p (x ₁ ,t ₁; x ₂ ,t ₂; …, x_m,t_m,).

Случайный процесс называется стационарным, если при сдвиге по времени на произвольную величину T функция распределения (а значит и плотность) не изменится. В этом случае плотность p (x,t) не зависит от времени: p (x,t) =p (x,t+T) =p (x, 0), а двумерная плотность p (x ₁, t ₁; x ₂, t ₂) зависит от разности t=t ₁ -t ₂. Введя автокорреляционную функцию случайного процесса K (t) = cov(X (t) ,X (t+t)), можно доказать, что для нее выполняются следующие свойства:

1) K (-t) =K (t);

2) |K (t)|£ K (0);

3) K (0) =DX.

Иногда функцию K (t) называют автоковариационной, а термин «автокорреляция» связывают с нормированной величиной r(t) =K (t)/ K (0).

Напомним, что для стационарного случайного процесса математическое ожидание m =EX (t) и дисперсия DX=E (X (t)-m) ² являются постоянными величинами. Если о случайном процессе известно, что EX и DX постоянны, а корреляционная функция зависит только от t (и не зависит от t), то случайный процесс называется стационарным в широком смысле.

Пусть значения временного ряда x_t (t = 1,2 ,...n) являются равноотстоящими по времени значениями стационарного случайного процесса X (t) с математическим ожиданием μ =EX =0 и корреляционной функцией K (τ) =E (X (t) X (t +τ)), при этом дисперсия DX=K (0)ºσ ². Несмещенной оценкой величины m является среднее по времени

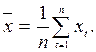
В качестве оценки корреляционной функции K (τ) при t= 0,1,2 ,...n- 1 можно принять величину

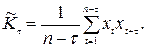
Важной характеристикой стационарного случайного процесса является спектральная плотность

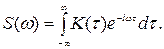(11.3)

Если, например,

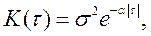
то

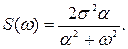
Из (11.3) следует, что

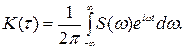
Функция K (t) четная, поэтому для спектральной плотности имеем также формулу:

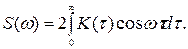
Для S (ω) принимается оценка

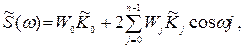
где весовые коэффициенты W_j вводятся для сглаживания случайных осцилляций вычисляемых значений S (ω). На практике вычисление корреляционных функций и спектральной плотности выполняется с использованием статистических компьютерных пакетов, например, системы Statistica.