2014-02-01
713
5.1. Функции и их характеристики
Наиболее популярные функции регрессии приведены в табл.5.1.
таблица 5.1
| Вид функции у |
Первая производная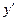 
| Коэффициент
эластичности
|
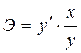
| 1.Линейная y=a+bx+c | b | bx /(a+bx) |
| 2.Парабола второй степени: y=a+bx+cx 2 +ε | b+ 2 cx | (b +2 cx) x /(a+bx + cx 2) |
| 3.Гиперболическая y=a+b / x+ε | -b / x 2 | -b /(ax+b) |
| 4.Показательная y=a·bx·ε | (ln b) abx | x ·ln b |
| 5.Степенная y=a·xb·ε | abxb- 1 | b |
| 6.Полулогарифмическая y=a+b ln x+ε | b / x | b /(a+b ln x) |
| 7.Логистическая y=a /(1+ b-cx+ε) | (a·b·c·e-cx)/(1+ be-cx)2 |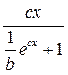 
|
| 8.Обратная y =1/(a+bx+ε) | -b /(a+bx)2 | -bx /(a+bx) |
5.2 Корреляция при нелинейной регрессии
Уравнение нелинейной регрессии дополняется показателем корреляции – индексом корреляции.
Для любых моделей, в том числе и нелинейных, показатель корреляции вычисляется так:
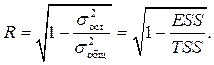
Если модель нелинейная относительно объясняющей переменной приводится к виду парной или множественной регрессии, то линейный коэффициент корреляции совпадает с индексом корреляции.
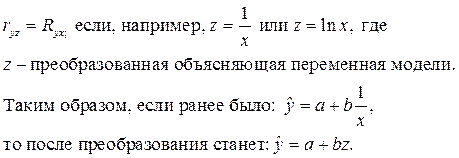
Иначе дело обстоит, если линеаризация связана с преобразованием результативной переменной у. В этом случае линейный коэффициент корреляции по преобразованным значениям признака числено не совпадает с индексом корреляции. Тем не менее, в большинстве практических случаев эти значения бывают достаточно близки.
Индекс детерминации R 2 можно использовать для расчёта F- статистики Фишера, по значению которой оценивается существенность уравнения в целом.
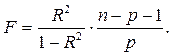
Пусть для некоторой зависимости построены линейные и нелинейные модели. Тогда индекс детерминации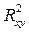 
можно сравнить с коэффициентом детерминации линейной модели 
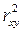.Чем больше кривизна линии регрессии, тем более 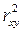будет меньше, чем 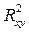и наоборот.Близость этих показателей означает, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию. Если разность 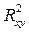–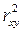не превышает 0,1; 0,15, то предположение о линейной форме связи вполне оправдано.В противном случае существенность этого различия оценивают по t – статистике Стьюдента.
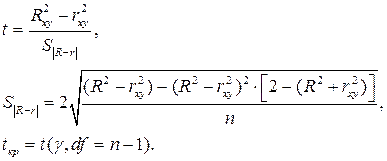
На практике считают, что если t < 2, то вполне подходит линейная регрессия.
