Системы одновременных уравнений

10.1. Виды переменных и уравнений СОУ

В экономических, социальных и финансовых науках объекты статистических исследований достаточно сложны. Каждое отдельное взятое уравнение множественной регрессии не может характеризовать истинные взаимосвязи между переменными модели системы.

Отсюда возникает необходимость создания СОУ (системы одновременных уравнений); ее особенность такова, что в одних уравнениях некоторая переменная рассматривается, как объясняющая, а в другое уравнение входит как объясняемая, т.е. зависимая переменная.

Примеры СОУ:

1. Модель спроса – предложения (см. рис. 10.1):

S

P

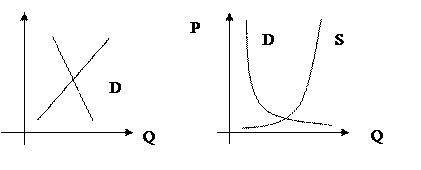
рис. 10.1

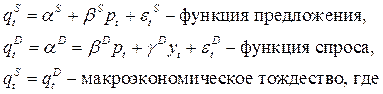
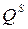– предложение, 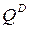- потребление, - доход.

2. Кейнсианская модель – модель формирования дохода (закрытая экономика без государственных расходов):

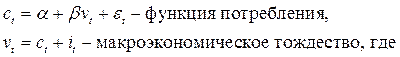
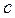- потребление, 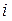- инвестиции, 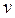- доход.

Переменные делят на 2 больших класса:

– экзогенные – переменные внешние по отношению к модели (объясняющие или факторные переменные),

– эндогенные – переменные, значения которых определяются внутри модели.

Экзогенные всегда предопределенны, то есть определены заранее, до рассмотрения уравнения. К предопределенным переменным также относят лаговые значения эндогенных переменных. Уравнения, описывающие модель рассмотренным выше образом, называются структурными уравнениями и тогда имеет смысл говорить о структурной форме модели (СФМ). Уравнения подразделяются на:

– поведенческие (функциональные),

– уравнения – тождества.

Первые из них описывают взаимодействие между переменными и содержат случайные составляющие, а также параметры, подлежащие оцениванию. Уравнения – тождества этого не содержат и выполняются в любом случае. Можно создать систему независимых уравнений, в которой каждая эндогенная переменная будут выражена только через экзогенные и предопределенные переменные плюс случайная составляющая. Такие уравнения называются уравнениями в приведенной форме, и говорят, что системы таких уравнений имеют приведенную форму (ПФМ).

СФМ (неполная): ПФМ (полная):

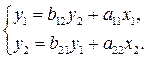
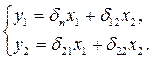
Структурную и приведенную формы, описываемые данными уравнениями, можно представить в виде графовой модели, как показано на рис.10.2. Видно, что СФМ представляет собой систему с перекрестными связями, а ПФМ – линейную систему с параллельными каналами.

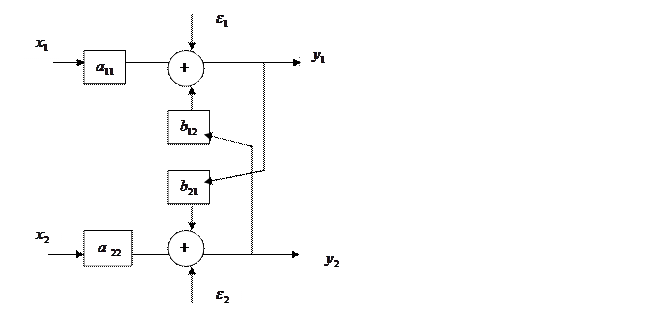
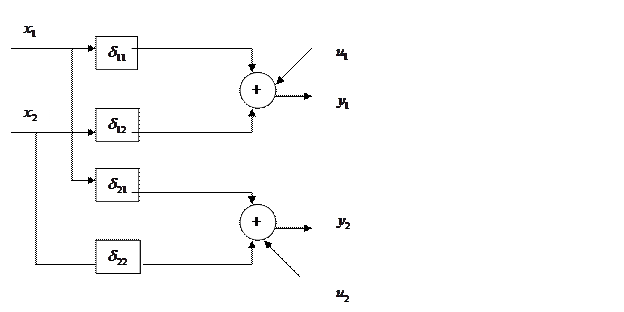
Рис. 10.2

В записанных выше системах для простоты случайные составляющие не включены, а все переменные взяты центрированными, чтобы в уравнении не было свободных членов. Напомним, что центрирование – это вычитание из истинного значения переменной ее среднего значения.

Для оценки параметров ПФМ можно использовать классический МНК, так как все уравнения независимы и для них выполняются условия Гаусса – Маркова.

К уравнениям СФМ применять непосредственно классический МНК нельзя, так как объясняющие переменные коррелируют со случайными составляющими. В связи с этим оценки могут получаться несостоятельными и смещенными. Следовательно, нужно использовать специальные методы методы оценки.

10.2. Проблемы идентификации

Пусть в некоторой системе содержится 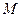экзогенных переменных и N эндогенных переменных. Тогда СФМ будет содержать 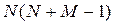параметров, подлежащих оценке, а ПФМ только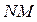. Рассмотрим эту систему:

СФМ:

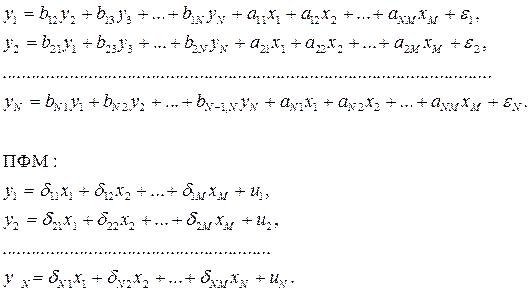
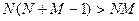для полных моделей, так как .

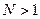В СФМ содержится N (N+M– 1) коэффициентов, а в ПФМ только NM коэффициентов и при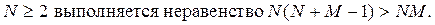

Очевидно, что из наличествующих коэффициентов ПФМ не удается однозначно определить все коэффициенты СФМ, если СФМ является полной. В таком случае говорят, что структурная модель не идентифицируется. Можно говорить о точной идентифицируемости, неидентифицируемости и сверхидентифицируемости (переопределенности) системы структурных уравнений и каждого уравнения в отдельности.

Система неидентифицируема, если неидентифицируемо хотя бы одно уравнение; система идентифицируема, если все ее уравнения идентифицируемы.

Пусть СОУ включает в себя N уравнений относительно N эндогенных переменных и пусть в системе имеется M экзогенных либо предопределенных переменных. Пусть количество эндогенных и экзогенных переменных в проверяемом уравнении равно n и m, соответственно. Переменные, не входящие в данное уравнение, но входящие в другие уравнения, называют исключенными переменными. Количество их равно N–n для эндогенных и M–m – для экзогенных переменных, соответственно. Тогда необходимое условие идентифицируемости для i– го уравнения будет иметь вид:

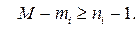
Достаточные условия идентифицируемости можно определить так:

1) в каждом уравнении структурной формы все переменные со своими коэффициентами переносятся в одну часть, при этом в другой части остается нуль;

2) для каждого i −го уравнения СФМ составляется матрица A коэффициентов при переменных, исключенных из данного уравнения, но входящих в другие уравнения;

3) вычисляется определитель этой матрицы и устанавливается ее ранг.

Если определитель отличен от нуля и ранг матрицы не меньше числа эндогенных переменных в системе минус единица (N –1), то уравнение идентифицируемо. При строгом неравенстве, то есть когда rank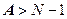, оно сверхидентифицируемо; при точном равенстве (rank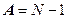) – точно идентифицируемо, а если rank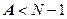, то уравнение неидентифицируемо и однозначно его коэффициенты определить нельзя. В последнем случае в неидентифицируемое уравнение следует ввести одну или несколько экзогенных переменных.

Пример:

	y 1	y 2	y 3	y 4	x 1	x 2	x 3	x4
I	-1			b 14	a 11
II		-1	b 23			a 22
III			-1	b 34			a 33
IV	b 41	b 42		-1				a 44

Для первого уравнения матрица A запишется:

-1	b 23	a 22
	-1		a 33
b 42				a 44

rank A = 3 = N – 1 = 4 – 1– уравнение I точно идентифицируемо.

10.3. Оценивание параметров структурной модели

Существуют следующие методы оценивания:

1) косвенный метод наименьших квадратов (КМНК),

2) двухшаговый метод наименьших квадратов (ДМНК),

3) трехшаговый метод наименьших квадратов (ТМНК),

4) метод максимального правдоподобия.

Рассмотрим первые два.

КМНК – этот метод применяется для точно идентифицируемой модели, так как связан с решением системы алгебраических уравнений, которое должно быть единственно. Этапы выполнения метода следующие:

- структурная форма преобразуется в приведенную,

- для каждого уравнения приведенной формы с помощью классического МНК оцениваются коэффициенты ,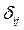

- коэффициенты приведенной модели трансформируются в коэффициенты структурной модели, путем решения системы алгебраических уравнений:

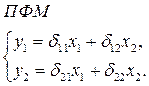
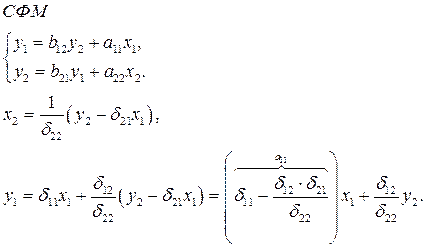
До сих пор мы для простоты выкладок использовали центрированные переменные, даже не отмечая факт центрированности особым значком (также для простоты). Теперь с целью моделирования реальной ситуации введем нецентрированые величины; тогда в уравнениях появятся свободные члены.

Нецентрированные величины:

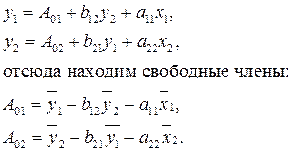
Если классический МНК применить к каждому уравнению структурной модели, в которой некоторые эндогенные переменные выступают в качестве объясняющих переменных (регрессоров), то оценки параметров получаются смещенными и несостоятельными в силу перекрестных корреляций между регрессорами и наличия случайных компонентов в регрессорах. В ряде случаев оценки могут вообще потерять экономический смысл.

Опасность таких результатов возрастает при увеличении числа эндогенных переменных в правой части системы, так как становится невозможно расщепить совместное влияние эндогенных переменных на отдельные составляющие и увидеть изолированные меры их воздействия на объясняемые переменные в соответствии с предпосылками обычного МНК.

ДМНК – этот метод применяют в тех случаях, когда структурная модель не является точно идентифицируемой. Основная идея метода состоит в том, что на основе приведенной модели (ПФМ) получают для каждой эндогенной переменной, которая в СФМ выступает в роли регрессора в том или ином уравнении, ее теоретическое значение, 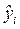и подставляют в таблицу наблюдений (выборку) вместо реально наблюдаемой переменной .

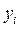Таким образом, после подстановки этих найденных теоретических значений 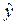в правые части уравнений СФМ к данным уравнениям уже можно применить классический МНК. Если система точно идентифицируема, то ДМНК дает этот же результат, что и КМНК. ДМНК – это наиболее общий и широко распространенный метод решения систем одновременных уравнений; он реализован в большинстве компьютерных статистических инструментов.