12.1. Метод скользящей средней
В основу метода скользящей средней (МА ─ moving average) для исключения флуктуаций временного ряда заложен следующий принцип: Если индивидуальный разброс члена ряда 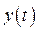 вокруг среднего сглаженного значения характеризуется дисперсией
вокруг среднего сглаженного значения характеризуется дисперсией 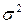 , то разброс среднего из n членов ряда
, то разброс среднего из n членов ряда 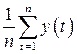 вокруг того же значения будет характеризоваться меньшей дисперсией
вокруг того же значения будет характеризоваться меньшей дисперсией 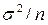 . Снижение дисперсии объясняется сглаживанием траектории ряда.
. Снижение дисперсии объясняется сглаживанием траектории ряда.
Для реализации метода МА выбирают определенную (как правило, нечетную) длину усреднения 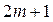 ,измеренную в числе следующих подряд членов ряда, подлежащего исследованию. При этом должно соблюдаться условие
,измеренную в числе следующих подряд членов ряда, подлежащего исследованию. При этом должно соблюдаться условие 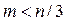 . Сглаженную функцию временного ряда
. Сглаженную функцию временного ряда 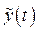 вычисляют по значениям
вычисляют по значениям 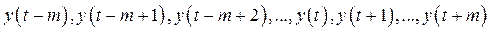 по следующей формуле:
по следующей формуле: 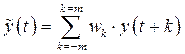 , где
, где 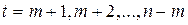 , а
, а
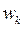 ─ некоторые положительные веса, сумма которых равна единице. Часто выбирают
─ некоторые положительные веса, сумма которых равна единице. Часто выбирают 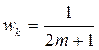 для всех значений k.
для всех значений k.
Рассмотрим пример (см. рис. 12.1). Пусть 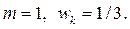
 | |||
 | |||
 I I I I I I I I I I I I I I I I
I I I I I I I I I I I I I I I I

 (2) I • I
(2) I • I


 (3) I • I
(3) I • I

 (4) I • I
(4) I • I
рис. 12.1
Число членов сглаженного ряда 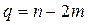 . Эту величину называют порядком преобразования по методу МА ─
. Эту величину называют порядком преобразования по методу МА ─ 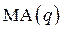 .
.
12.2. Регрессионная модель и метод конечных разностей
Кроме метода МА для аналитического сглаживания флуктуирующего временного ряда используют также классический МНК, то есть строят однофакторную регрессионную модель с объясняющей переменной t и метод конечных разностей. Последний метод основан на том, что вычисление конечных разностей различных порядков для выражений в дискретном времени аналогично многократному дифференцированию выражений в непрерывном времени. Очевидно, что многократное дифференцирование приводит к устранению сначала ─ постоянной составляющей, затем ─ скорости, далее ─ ускорения и так далее. Конечные разности вычисляются так:

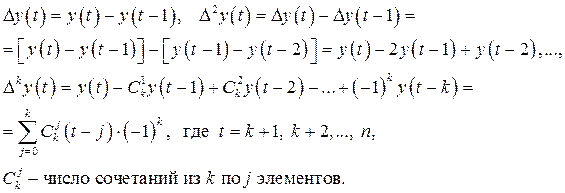
12.3. Стационарные и нестационарные временные ряды
Создание модели, адекватно описывающей поведение остатков 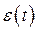 анализируемого ряда
анализируемого ряда 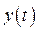 , проводят обычно в рамках класса стационарных временных рядов. Ряд
, проводят обычно в рамках класса стационарных временных рядов. Ряд 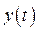 называют строго стационарным, если совместное распределение вероятностей наблюдений
называют строго стационарным, если совместное распределение вероятностей наблюдений 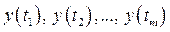
и наблюдений 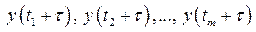 одинаково для любых m,
одинаково для любых m,
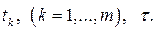 Таким образом, свойства строго стационарного ряда не изменяются при изменении начала отсчета времени и числа наблюдений.
Таким образом, свойства строго стационарного ряда не изменяются при изменении начала отсчета времени и числа наблюдений.
В частности, при 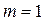 строгая стационарность ряда
строгая стационарность ряда 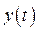 обуславливает то, что закон распределения вероятностей случайной величины
обуславливает то, что закон распределения вероятностей случайной величины 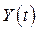 не зависит от t; следовательно, от t не зависят и основные числовые характеристики ряда: среднее значение
не зависит от t; следовательно, от t не зависят и основные числовые характеристики ряда: среднее значение 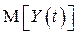 и дисперсия
и дисперсия 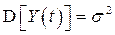 .
.
Ряд 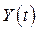 называют слабо стационарным, если его среднее значение и дисперсия не зависят от t, но не более того. Строго стационарный ряд одновременно слабо стационарен, но не наоборот. Для стационарных рядов характерно монотонное убывание автокорреляционной функции.
называют слабо стационарным, если его среднее значение и дисперсия не зависят от t, но не более того. Строго стационарный ряд одновременно слабо стационарен, но не наоборот. Для стационарных рядов характерно монотонное убывание автокорреляционной функции.
Нестационарным называют ряд, отличающийся от стационарного на неслучайную, зависящую от t составляющую.
При строгой стационарности совместные двумерные распределения пар 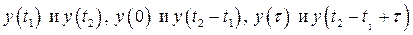 совпадают и зависят только от
совпадают и зависят только от 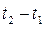 . Ковариация
. Ковариация 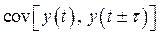 будет зависеть только от временного сдвига
будет зависеть только от временного сдвига 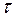 .
.
12.4. Преобразования ARMA и ARIMA
Сочетание авторегрессионного преобразования  и скользящей средней
и скользящей средней 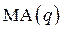 называют ARMA─моделью (ARMA─autoregression & moving average model). Модель
называют ARMA─моделью (ARMA─autoregression & moving average model). Модель 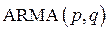 имеет вид:
имеет вид:
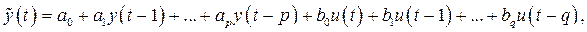
где 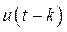 ─ независимые друг от друга нормально распределенные случайные величины с нулевым матожиданием и постоянной дисперсией.
─ независимые друг от друга нормально распределенные случайные величины с нулевым матожиданием и постоянной дисперсией.
Преобразование ARMA в сочетании с переходом от объемных величин к приростным называется ARIMA─преобразованием или ARIMA ─ моделью (autoregression & integrated moving average model). Эту модель также называют моделью Бокса─Дженкинса. В некоторых случаях такое преобразование позволяет получить более точную и явную модель зависимости. ARIMA─модель обычно используют для описания временных рядов со следующими свойствами: ряд аддитивно включает составляющую 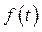 , имеющую вид полинома от t; ряд, полученный из исходного ряда после применения к нему метода конечных разностей k раз, может быть описан моделью
, имеющую вид полинома от t; ряд, полученный из исходного ряда после применения к нему метода конечных разностей k раз, может быть описан моделью
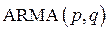 .
.
Таким образом, модель 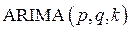 может быть записана в виде:
может быть записана в виде:
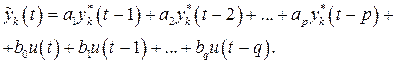
Величины 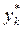 представляют собой конечные разности порядка k переменной
представляют собой конечные разности порядка k переменной 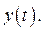
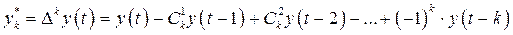 .
.
 2014-02-01
2014-02-01 766
766








