При исследовании экономических процессов часто приходится моделировать ситуации, когда значение 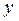 в текущий момент времени
в текущий момент времени 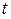 формируется под воздействием факторов, действовавших в прошлые моменты времени:
формируется под воздействием факторов, действовавших в прошлые моменты времени: 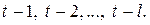 Задержанные значения факторов называют лаговыми значениями, а наибольшую величину задержки называют длиной лага Модель вида
Задержанные значения факторов называют лаговыми значениями, а наибольшую величину задержки называют длиной лага Модель вида 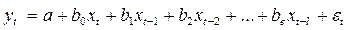
называют моделью с распределенным лагом. В качестве объясняющих причин также могут выступать лаговые значения зависимой переменной 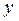 .
.
Модель вида 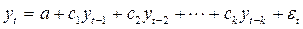
называются моделями авторегрессии. Может быть составлена такая модель общего вида:
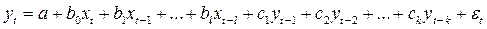 .
.
Она может быть разложена на 2 составляющие:
- составляющая с распределенным лагом длины 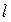 ,
,
- авторегрессионная составляющая порядка 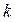 .
.
11.1. Интерпретация параметров модели с распределенным лагом
Коэффициент 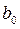 характеризует средние абсолютное изменение объясняемой переменной
характеризует средние абсолютное изменение объясняемой переменной 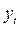 при изменении регрессора
при изменении регрессора 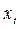 на одну единицу собственного измерения в момент
на одну единицу собственного измерения в момент 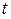 без учета воздействия лаговых значений переменной x. Поэтому
без учета воздействия лаговых значений переменной x. Поэтому 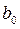 называют – краткосрочным мультипликатором. Сумму коэффициентов от
называют – краткосрочным мультипликатором. Сумму коэффициентов от 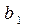 до
до 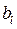 называют долгосрочным мультипликатором, его обозначают
называют долгосрочным мультипликатором, его обозначают 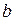 без индекса.
без индекса.
Относительные коэффициенты такой модели выражаются формулой.
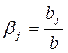 .
.
Если все 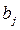 имеют знак «+» и значение каждого коэффициента заключено между 0 и 1, а сумма всех коэффициентов от
имеют знак «+» и значение каждого коэффициента заключено между 0 и 1, а сумма всех коэффициентов от 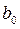 до
до 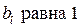 , то можно ввести следующие характеристики:
, то можно ввести следующие характеристики:
1.Средний лаг 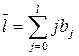 , где
, где 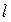 - средний период, в течение которого будет происходить изменение под воздействием изменения. Небольшая величина
- средний период, в течение которого будет происходить изменение под воздействием изменения. Небольшая величина 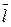 говорит о быстром реагировании y на изменение фактора и наоборот.
говорит о быстром реагировании y на изменение фактора и наоборот.
2.Медианный лаг 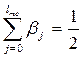 ; он представляет такой период, в течение которого, начиная с момента
; он представляет такой период, в течение которого, начиная с момента 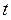 , будет реализована половина общего воздействия фактора на объясняемую переменную.
, будет реализована половина общего воздействия фактора на объясняемую переменную.
Применение классического МНК к модели с распределенным лагом осложняется следующими причинами:
1) текущие и лаговые значения фактора обычно тесно связаны друг с другом и оценка параметров будет производиться в условиях сильной мультиколлинеарности;
2) при большой длине лага снижается число наблюдений и увеличивается число регрессоров;
3) в модели с распределенным лагом часто возникает проблема автокорреляции в остатках.
11.2. Интерпретация параметров модели авторегрессии
Рассмотрим простейшую модель авторегрессии, а именно модель первого порядка 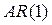 :
:
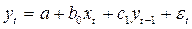 .
.
Так же, как и в модели с распределением лагом, коэффициент 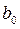 является краткосрочным мультипликатором. Долгосрочный мультипликатор будет вычисляется как сумма членов геометрической прогрессии:
является краткосрочным мультипликатором. Долгосрочный мультипликатор будет вычисляется как сумма членов геометрической прогрессии:
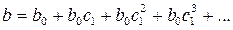
К моменту времени 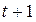 результативный признак
результативный признак 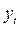 изменяется под воздействием изменения фактора
изменяется под воздействием изменения фактора 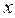 в момент времени
в момент времени 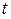 на величину
на величину 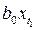 , а
, а
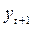 – под воздействием своего изменения в непосредственно предшествующий момент изменяется на величину
– под воздействием своего изменения в непосредственно предшествующий момент изменяется на величину 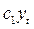 . Таким образом, результирующее изменение результативного признака в момент
. Таким образом, результирующее изменение результативного признака в момент 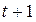 будет равно
будет равно 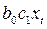 и так далее.
и так далее.
Произведение 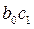 можно рассматривать как промежуточный мультипликатор.
можно рассматривать как промежуточный мультипликатор.
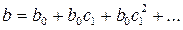 – эта прогрессия возникает в силу рекуррентности формулы авторегрессии и она будет являться бесконечной. Используя формулу для бесконечно убывающей геометрической прогрессии, которая является сходящимся рядом, можно найти сумму этого ряда:
– эта прогрессия возникает в силу рекуррентности формулы авторегрессии и она будет являться бесконечной. Используя формулу для бесконечно убывающей геометрической прогрессии, которая является сходящимся рядом, можно найти сумму этого ряда:
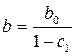 , где
, где 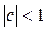 .
.
Заметим, что такая интерпретация коэффициентов регрессии и расчет долгосрочного мультипликатора основаны на предположении бесконечного лага.
11.3. Соображения о выборе лаговых структур в модели с распределенным лагом
Текущее значение фактора 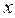 и его лаговые значения оказывают на результативный признак
и его лаговые значения оказывают на результативный признак 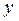 различное по силе воздействие. В большинстве моделей, описывающих реальные экономические процессы, коэффициенты регрессии при лаговых переменных убывают с ростом величины лага, но это не обязательно.
различное по силе воздействие. В большинстве моделей, описывающих реальные экономические процессы, коэффициенты регрессии при лаговых переменных убывают с ростом величины лага, но это не обязательно.
Вообще говоря, в большинстве случаев строят предположения о структуре лага на основе экономической теории или на результатах эмпирических исследований.
11.4. Полиномиальные лаговые структуры Алмон
Рассмотрим модель, в которой распределенный лаг имеет конечную длину 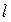 . Зависимость коэффициентов регрессии
. Зависимость коэффициентов регрессии 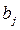 от величины лага описывается полиномом, в общем случае, некоторой степени
от величины лага описывается полиномом, в общем случае, некоторой степени 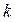 .
.
Для полинома 1-ой степени: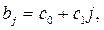
2-ой степени: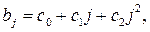
3-ей степени: 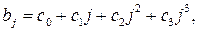
4-ой степени: 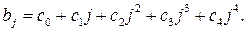
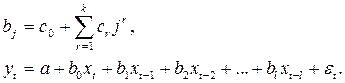
В развернутом виде коэффициенты перепишутся так:
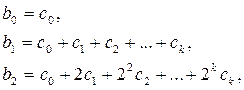
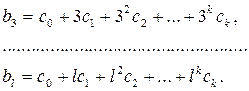
Тогда уравнение можно записать таким образом:
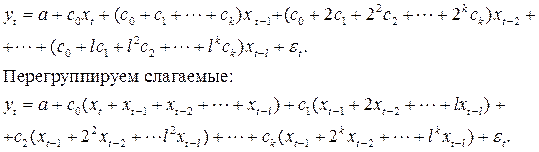
Суммы в скобках последнего выражения можно принять за новые переменные z 0, z 1, …, z k и тогда получим уравнение:
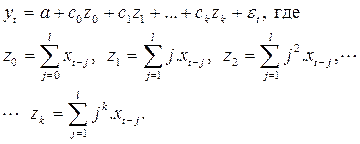
Чтобы рассчитать параметры модели с распределенным лагом нужно выполнить следующие действия:
1) определить длину лага 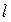 . Это можно сделать на основе имеющегося опыта или перебрать несколько значений
. Это можно сделать на основе имеющегося опыта или перебрать несколько значений 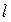 ; обычно от 2 до 5,
; обычно от 2 до 5,
2) установить степень полинома 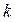 ; обычно от 2 до 4,
; обычно от 2 до 4,
3) по записанным выше формулам 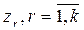 и таблице наблюдений, содержащей значения
и таблице наблюдений, содержащей значения 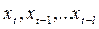 , рассчитать значения новых переменных
, рассчитать значения новых переменных 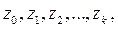
4) выполнить регрессию 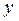 на набор переменных
на набор переменных 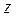 , и определить коэффициенты
, и определить коэффициенты 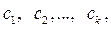
5) по формулам для 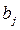 рассчитать все значения параметров исходной модели:
рассчитать все значения параметров исходной модели: 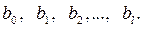
Несмотря на значительную привлекательность описанного выше метода, существуют следующие проблемы:
1. Не всегда легко выбрать длину лага 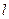 , но лучше ориентироваться на максимально возможную длину лага (в разумных пределах), чем сразу ограничиваться лагами малой длины. В противном случае можно потерять существенный регрессор, то есть составить неправильную спецификацию модели. Влияние потерянного существенного регрессора будет сказываться в остатках, то есть в модели не станут соблюдаться предпосылки МНК по случайности остатков. Оценки параметров могут оказаться не только неэффективными, но и смещенными. Если лаг выбран слишком длинным, то в модель могут попасть несущественные факторы; эффективность оценок параметров может снизиться, но они останутся несмещенными. Если аналитик располагает достаточными ресурсами времени и вычислительными ресурсами, можно построить несколько моделей с различными значениями
, но лучше ориентироваться на максимально возможную длину лага (в разумных пределах), чем сразу ограничиваться лагами малой длины. В противном случае можно потерять существенный регрессор, то есть составить неправильную спецификацию модели. Влияние потерянного существенного регрессора будет сказываться в остатках, то есть в модели не станут соблюдаться предпосылки МНК по случайности остатков. Оценки параметров могут оказаться не только неэффективными, но и смещенными. Если лаг выбран слишком длинным, то в модель могут попасть несущественные факторы; эффективность оценок параметров может снизиться, но они останутся несмещенными. Если аналитик располагает достаточными ресурсами времени и вычислительными ресурсами, можно построить несколько моделей с различными значениями 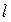 и сравнить их качество.
и сравнить их качество.
2. При выборе степени полинома 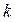 обычно ограничиваются значениями 2,3,4, руководствуясь следующим соображением: степень полинома
обычно ограничиваются значениями 2,3,4, руководствуясь следующим соображением: степень полинома 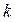 должна быть на единицу больше, чем число экстремумов в структуре лага.
должна быть на единицу больше, чем число экстремумов в структуре лага.
3. Переменные 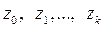 представляют собой линейные комбинации лаговых значений фактора x и поэтому будут сильно коррелировать между собой, если имеет место высокая степень связи между исходными данными
представляют собой линейные комбинации лаговых значений фактора x и поэтому будут сильно коррелировать между собой, если имеет место высокая степень связи между исходными данными 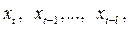 то есть имеет место автокорреляция во временном ряду объясняющих переменных.
то есть имеет место автокорреляция во временном ряду объясняющих переменных.
Следует заметить, что при определении параметров 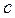 с помощью МНК мультиколлинеарность переменных
с помощью МНК мультиколлинеарность переменных 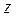 скажется меньше, чем мультиколлинеарность переменных
скажется меньше, чем мультиколлинеарность переменных 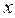 при непосредственном определении параметров
при непосредственном определении параметров 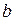 из исходного уравнения.
из исходного уравнения.
Преимущества метода лаговых структур Алмон:
1. Существует возможность воспроизвести достаточно разнообразные структуры лага с помощью подбора полинома нужной степени.
2. При небольшом количестве переменных 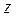 можно построить модели с распределенным лагом произвольной длины.
можно построить модели с распределенным лагом произвольной длины.
11.5. Геометрические структуры Койка
В модели Койка предполагается, что в уравнении регрессии имеет место бесконечный лаг, но коэффициенты при лаговых переменных убывают в геометрической прогрессии, отсюда название – геометрическая структура Койка.
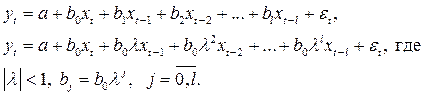
Последнее уравнение справедливо для всякого момента времени, в том числе и для момента 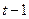 ; поэтому можно записать:
; поэтому можно записать:
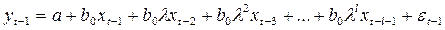 .
.
Умножим последнее уравнение на 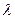 и вычтем из предыдущего:
и вычтем из предыдущего:
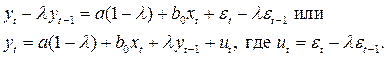
Краткосрочный мультипликатор рассчитывается как сумма бесконечно убывающей геометрической прогрессии
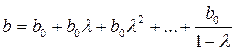 .
.
Если считать, что объясняющая переменная 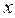 стремится к равновесию
стремится к равновесию 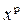 , то значения
, то значения 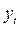 и
и 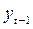 будут также стремиться к своему равновесному значению
будут также стремиться к своему равновесному значению 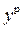 :
:
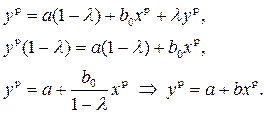
Здесь возможны следующие проблемы:
В уравнении регрессии регрессор 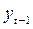 в принципе носит случайный характер, так как содержит остаток
в принципе носит случайный характер, так как содержит остаток 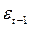 , а значит, нарушается одна из предпосылок МНК. Для случайных остатков
, а значит, нарушается одна из предпосылок МНК. Для случайных остатков 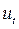 будет иметь место автокорреляция. Если учесть случайный характер регрессора
будет иметь место автокорреляция. Если учесть случайный характер регрессора 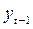 и автокорреляция в остатках
и автокорреляция в остатках 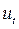 выражена достаточно сильно, то оценки параметров, полученные с помощью классического МНК, могут оказаться несостоятельными и смещенными.
выражена достаточно сильно, то оценки параметров, полученные с помощью классического МНК, могут оказаться несостоятельными и смещенными.
Средний и медианный лаги модели Койка вычисляются таким образом:
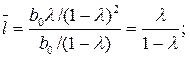
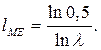
Видно, что если 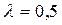 то
то 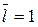 . При
. При 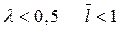 ; при
; при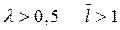 . Величину
. Величину 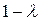 объясняют как скорость, с которой происходит во времени адаптация объясняемой переменной
объясняют как скорость, с которой происходит во времени адаптация объясняемой переменной 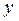 к изменению объясняющей переменной
к изменению объясняющей переменной 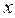 .
.
11.6. Оценка параметров авторегрессионных моделей первого порядка (AR(1)–моделей)
Такая модель выглядит следующим образом: 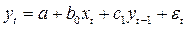 .
.
Авторегрессионная модель довольно часто используется в эконометрических исследованиях, но при их построении возникает 2 проблемы:
Первая проблема касается выбора метода оценки параметров: так как в правой части регрессионного уравнения присутствует лаговая переменная 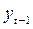 , то тем самым нарушается предпосылка МНК о делении переменных на стохастическую объясняемую переменную и детерминированную объясняющую переменную;
, то тем самым нарушается предпосылка МНК о делении переменных на стохастическую объясняемую переменную и детерминированную объясняющую переменную;
Вторая проблема состоит в том, что регрессор 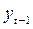 явным образом коррелирует с остатком
явным образом коррелирует с остатком 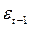 и тем самым нарушается 4–е условие Гаусса-Маркова. Поэтому применение классического МНК для оценки параметров этой модели приводит к получению смещенной оценки коэффициента c 1.
и тем самым нарушается 4–е условие Гаусса-Маркова. Поэтому применение классического МНК для оценки параметров этой модели приводит к получению смещенной оценки коэффициента c 1.
Популярным методом расчета параметров AR– модели является метод инструментальных переменных (ИП). Суть этого метода заключается в следующем: та переменная в правой части AR–модели, для которой нарушается предпосылка МНК, заменяется на другую переменную, которая эту предпосылку не нарушает. Применительно к 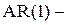 модели заменить на инструментальную переменную следует лаговую переменную
модели заменить на инструментальную переменную следует лаговую переменную 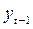 . Эта переменная должна обладать двумя свойствами:
. Эта переменная должна обладать двумя свойствами:
1) сильно коррелировать с 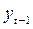 ,
,
2) быть детерминированной и не коррелировать с остатком.
Рассмотрим два способа получения инструментальной переменной:
Способ 1. Так как в модели переменная 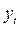 зависит не только от
зависит не только от 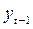 , но и от фактора
, но и от фактора 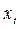 , то можно построить модель с одним регрессором
, то можно построить модель с одним регрессором 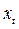 и теоретическое значение
и теоретическое значение 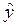 , полученное с помощью такой модели, можно использовать в качестве инструментальной переменной.
, полученное с помощью такой модели, можно использовать в качестве инструментальной переменной.
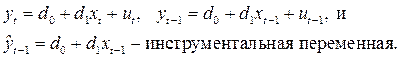
Параметры 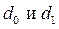 в последнем уравнении можно найти с помощью классического МНК. Здесь оценка
в последнем уравнении можно найти с помощью классического МНК. Здесь оценка 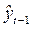 тесно коррелирует с наблюдаемой переменной
тесно коррелирует с наблюдаемой переменной 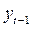 и является линейной функцией от фактора
и является линейной функцией от фактора 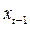 , для которого 4–е условие Гаусса–Маркова не нарушается. Следовательно, ИП
, для которого 4–е условие Гаусса–Маркова не нарушается. Следовательно, ИП 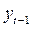 также не будет коррелировать с остатком
также не будет коррелировать с остатком 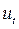 . Таким образом, оценки параметров уравнения
. Таким образом, оценки параметров уравнения 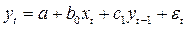 можно найти из соотношения
можно найти из соотношения
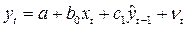 .
.
Способ 2. Подставим в AR – уравнение вместо 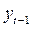 его выражение
его выражение
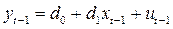 , тогда получим:
, тогда получим:
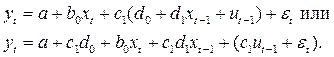
Мы получили уравнение модели с распределенным лагом, для которой можно применить классический МНК.
В результате последовательного проведения двух регрессий мы получаем следующие значения:
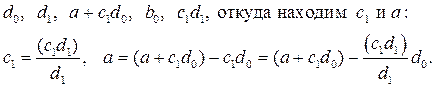
Практическая реализация метода инструментальных переменных осложняется следующими обстоятельствами:
– при способе 1 возникает интеркорреляция между переменными 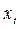 и
и 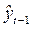 ; так как
; так как 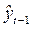 функционально связана с
функционально связана с 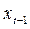 , то можно ожидать упомянутую выше интеркорреляцию.
, то можно ожидать упомянутую выше интеркорреляцию.
– при способе 2 может помешать такое обстоятельство, что 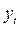 в исходной модели больше коррелирует с
в исходной модели больше коррелирует с 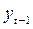 , чем с
, чем с 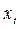 . Тогда модель
. Тогда модель 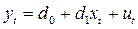 , а значит и модель
, а значит и модель 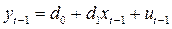 будут не вполне достоверно представлять переменную
будут не вполне достоверно представлять переменную 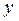 в правой части для модели
в правой части для модели 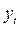 по второму способу.
по второму способу.
Эти проблемы иногда удается смягчить путем включения в модель временного фактора 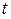 в качестве независимой переменной.
в качестве независимой переменной.
11. 7. Модель адаптивных ожиданий
Методы, которые созданы для построения и анализа DL– и AR– моделей, можно использовать для верификации макроэкономических моделей, учитывающих определенные ожидания относительно значений экономических показателей, включенных в модель в момент времени t. Рассмотрим модель адаптивных ожиданий вида:
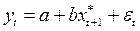 .
.
Здесь yt – фактическое значение результативного признака (объясняемой переменной), а 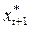 – ожидаемое значение факторного признака в момент t+ 1.
– ожидаемое значение факторного признака в момент t+ 1.
Механизм формирования ожиданий в этой модели следующий:
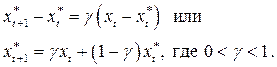
Таким образом, ожидаемое значение фактора в некоторый момент времени t+ 1 представляет собой средневзвешенное его фактического и ожидаемого значений в предыдущий период t. Видно, что в каждый период t+ 1 ожидания корректируются на некоторую долю 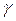 от разности между фактическим и ожидаемым значениями фактора в предыдущий период. Параметр
от разности между фактическим и ожидаемым значениями фактора в предыдущий период. Параметр 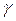 называют коэффициентом ожиданий. Чем ближе он к единице, тем в большей степени реализуются ожидания экономического агента, и наоборот, приближение коэффициента
называют коэффициентом ожиданий. Чем ближе он к единице, тем в большей степени реализуются ожидания экономического агента, и наоборот, приближение коэффициента 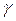 к нулю свидетельствует об устойчивости существующих тенденций. Это означает, что условия, доминирующие сегодня, будут сохраняться на будущие периоды времени.
к нулю свидетельствует об устойчивости существующих тенденций. Это означает, что условия, доминирующие сегодня, будут сохраняться на будущие периоды времени.
В уравнение 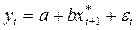 подставим выражение
подставим выражение 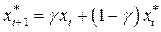
 и получим
и получим 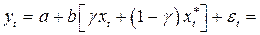
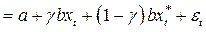 . (*)
. (*)
Далее, если рассматриваемая изначально модель имеет место для момента или периода t, то она очевидно будет действовать и в период t– 1, а значит мы можем записать: 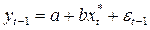 . Умножим последнее уравнение на
. Умножим последнее уравнение на 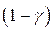 и вычтем из уравнения (*):
и вычтем из уравнения (*):
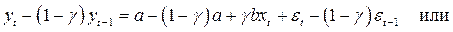
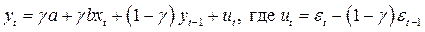 .
.
Теперь мы можем определить параметры последнего авторегрессионного уравнения и легко перейти к исходной модели. По найденному в результате регрессионного анализа коэффициенту 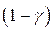 отыскивается коэффициент
отыскивается коэффициент 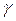 , по коэффициенту
, по коэффициенту 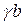 при
при 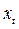 отыскивается коэффициент b, а по свободному члену
отыскивается коэффициент b, а по свободному члену 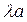 отыскивается свободный член исходного уравнения a.
отыскивается свободный член исходного уравнения a.
Различие между начальным и последним уравнениями состоит в том, что первая модель включает в себя ожидаемое значение фактора 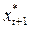 и к ней нельзя применять классические статистические методы. Последняя же модель включает в себя только фактические, то есть наблюдаемые значения переменных и ее параметры можно определить.
и к ней нельзя применять классические статистические методы. Последняя же модель включает в себя только фактические, то есть наблюдаемые значения переменных и ее параметры можно определить.
Однако, как и в случае с моделью Койка, применение классического МНК приведет к смещению оценок параметров ввиду наличия в правой части лагового значения результативного признака 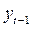 .
.
 2014-02-01
2014-02-01 826
826








