Пример оценки надежности реконструируемого здания

Анализ надежности реконструируемых зданий рационально проводить с применением численных методов решения уравнений. Наиболее простой является двухэлементная система «основание- фундамент», на примере которой покажем ее количественные характеристики надежности в зависимости от времени эксплуатации и состояния элементов. Выбор данной системы неслучаен, так как она определяет прежде всего необходимость и объем проведения восстановительных работ для обеспечения заданного уровня надежности здания в целом, а также позволяет прогнозировать поведение системы во времени. В то же время эта система является наиболее ответственным элементом здания, определяющим его эксплуатационную надежность и долговечность.Зависимость (4.9) может быть распространена на многоэлементные системы,включающие стены перекрытия и другие несущие конструкции. При этом учитываются соответствующие графы переходов.

В качестве исходных данных берутся следующие параметры: t ₁ - среднее время от момента постройки до момента, когда в грунте возникают опасные физико-механические изменения; t ₂ - среднее время между возникновением опасных нарушений физико-механических свойств грунта и потерей несущей способности фундамента; t ₃ - средняя продолжительность функционирования фундамента при условии, что грунт не подвергается никаким нарушениям. Для расчетов брались следующие значения параметров (в годах)

t ₁ = 20; 30; 40; 50; t ₂= 10; 20; 50; t ₃= 50; 100.

Таким образом, получены 24 кривые, приведенные на рис. 4.19.

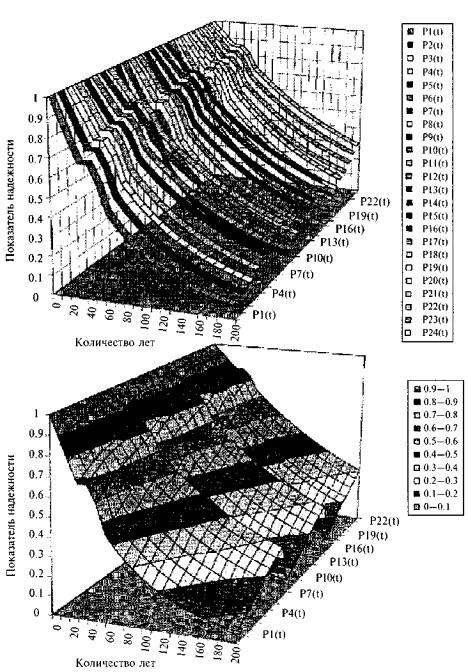
Рис. 4.19. Графики функций надежности в Р-мерном пространстве

Анализ показывает, что функция надежности монотонно убывает со временем. Кроме того, все кривые в промежутке между 30 и 50 годами меняются медленно, а после 60 лет ведут себя как экспоненты.

При выполнении реконструктивных работ без изменения объема здания и технологических нагрузок, т.е. когда сохраняется прежняя расчетная схема, оценка надежности производится по зависимости (4.9) с введением временных параметров, отвечающих уровню конструктивно-технологических решений.

Пусть, например, в возрасте t лет здание подвергается реконструкции, и при этом проводятся работы по укреплению фундаментов и грунтов основания. Результат этих работ таков, что параметры t ₁, t ₂, t ₃ принимают значения 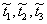. Тогда функция надежности реконструируемой системы получается в результате склеивания двух кривых

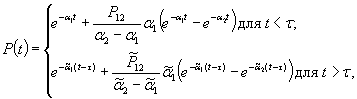
где a ₁, a ₂, Р ₁₂находятся по формулам (4.8), а 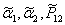-по тем же формулам с заменой t_i на 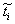(i = 1,2,3).

На рис. 4.20, а приведены графики функции надежности здания до реконструкции и после проведения реконструктивных работ. Реконструкция проводится в возрасте 100 лет, и значения после реконструкции приближаются к первоначальным.

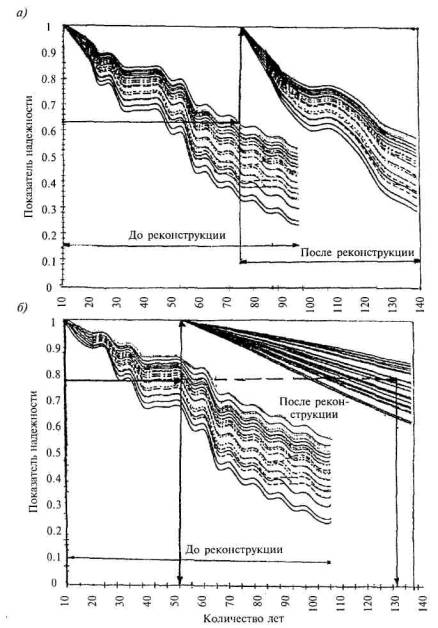
Рис. 4.20. Графики изменения показателя надежности зданий до и после реконструкции
а - при сохранении конструктивной схемы без изменений строительного объема; б -то же, при усилении конструктивных элементов и использовании встроенных строительных систем

Анализ графиков функций надежности показывает, что в целом система при начальной функции надежности,равной единице, постепенно снижает этот показатель до определенного минимума,который является предельным и служит основанием для проведения восстановительных (реконструктивных) работ. Продолжительность реконструкции обеспечивает восстановление первоначальных характеристик, но с некоторым снижением надежности, которое является следствием длительной эксплуатации некоторых невосстанавливаемых элементов здания.

Изменение надежности после реконструктивного периода с незначительными отклонениями повторяет характер кривых дореконструктивного периода эксплуатации здания.

Более низкая степень снижения показателя надежности (рис. 4.20, б) после реконструкции достигается в результате замены сменяемых конструкций на более долговечные, усиления фундаментов, стен, замены перекрытий и т.п. В совокупности комплекс реконструктивных работ повышает эксплуатационную надежность и продляет срок службы здания,обеспечивая менее интенсивное падение показателя надежности. Как правило, повышение капитальности конструктивных элементов способствует безотказной работе здания в достаточно большом промежутке времени.

Полученные зависимости при использовании достаточного количества статистических данных позволяют прогнозировать снижение надежности элементов и здания в целом, а при возникновении экстремальных условий - аварийные ситуации.

Таким образом, с учетом случайного характера воздействия на строительные конструкции предложена и изучена физическая модель надежности реконструируемых зданий. При этом необходимо учитывать две группы факторов: внутреннего характера, включая режимы эксплуатационного воздействия, а также внешнего, существенно влияющих на изменение физико-механических характеристик конструктивных элементов.

Экспоненциальный характер снижения надежности во времени практически преобладает для всех типов зданий,дойдя до порогового значения (отказа), после предотвращения которого(восстановления) система приобретает требуемую надежность. Характер возникновения отказов зависит от режимов эксплуатации зданий. Как правило,имеют место последовательные и постепенные отказы, и только в критических случаях наблюдаются внезапные отказы, вызванные потерей несущей способности конструктивных элементов в короткий срок эксплуатации. Они являются критическими и приводят к потере работоспособности элементов или в целом здания.

Анализ надежности и долговечности реконструируемых зданий должен опираться на описание функционирования объекта как сложной системы. Математически это означает рассмотрение многомерных случайных процессов. При этом отказ возникает при попадании этого процесса в некоторое критическое множество.

При наличии ремонтных работ,предполагающих полное восстановление объекта с точки зрения надежностных характеристик, функция надежности хорошо приближается к экспонентной. Для использования этого результата необходимо знать два параметра: среднее время между восстановительными работами и вероятность отказа в течение этого промежутка времени.

В случаях когда ремонтные работы либо не ведутся, либо не полностью восстанавливают объект с точки зрения его надежностных характеристик, эти параметры с течением времени только ухудшаются.В качестве модели, описывающей функционирование таких объектов, предлагаются иерархические процессы. Для них функция надежности вычисляется с помощью рекуррентной формулы.

Предложенные методики позволяют оценивать долговечность зданий до и после реконструкции при наличии довольно большого числа исходных данных. Часть из них может быть получена на основании статистических данных, а часть - с использованием результатов натурных обследований, расчетных методов строительной механики в сочетании с теорией случайных процессов. Оценка надежности и долговечности реконструированных зданий должна учитывать интенсивность различных воздействий внешнего и внутреннего характера.