Иерархические модели надежности

Оценка среднего времени до возникновения отказа

Для многих практически важных случаев функция надежности может быть оценена, если известно среднее время достижения критического множества, т.е. среднее время эксплуатации объекта до полной потери несущей способности. Вернемся к модели, описанной в § 4.1.

Пусть т (х)- среднее время до попадания в множество Q из состояния 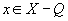. Для функций т (х)выполняется система уравнений

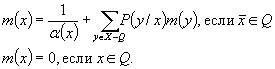(4.17)

Эта система линейных алгебраических уравнений состоит из конечного множества уравнений, так что ее решение не представляет собой значительных трудностей.

Пример5. Для наглядности рассмотрим объект, описанный ранее, с графом переходов (рис. 4.11).

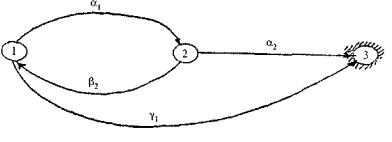
Рис. 4.11. Граф переходов для примера 5

Здесь

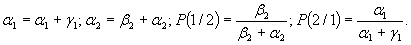
Система (4.17) принимает вид

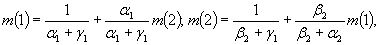
откуда

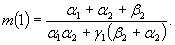(4.18)

Если g ₁ = 0, a ₂® 0, как это было в предыдущем параграфе, то асимптотика среднего времени эксплуатации

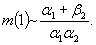(4.19)

что совпадает с зависимостью(4.15).

Метод наиболее вероятных траекторий

Асимптотические методы при оценке надежности объектов применимы, когда имеются неоднократные восстановления (регенерации) объекта.

Если предположить, что объект не ремонтируется или ремонты не возвращают его в первоначальное состояние, а только задерживают в том, в котором он уже находился, то состояния координат процесса могут быть перенумерованы таким образом, что с течением времени их значения только увеличиваются.

На рис. 4.12 показана типичная траектория такого процесса.

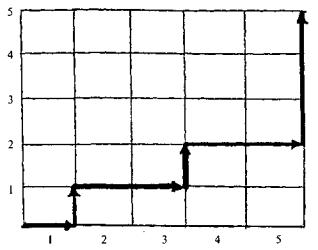
Рис. 4.12. Пример траектории иерархического процесса

По каждой координате возможно только увеличение. На рис. 4.12 показано движение вправо и вверх, но не вниз и влево. Процессы такого рода никогда не возвращаются в состояние, в котором они уже были.

Граф переходов таких процессов не имеет петель и выглядит, как показано на рис. 4.13.

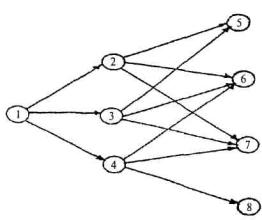
Рис. 4.13. Граф переходов в различные состояния

Такие процессы можно назвать иерархическими, поскольку все множество состояний разбивается на классы К ₁, К ₂,..., K_i и движение возможно только из одного класса в другой или в критическое множество (рис. 4.14).

Рис. 4.14. Иерархический процесс
К - классы состояний

Задачи теории надежности для таких процессов весьма своеобразны, и для них не работает асимптотическая теория. Сразу заметим, что система (4.1)может быть решена рекуррентно. В самом деле, введем двойную нумерацию для состояний, перенумеровав классы и состояния внутри класса, так что состояние (i, j)означает i -е состояние j -го класса. При такой нумерации вместо рис.4.13 будем иметь схему, представленную на рис. 4.15.

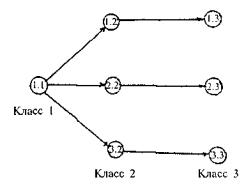
Рис. 4.15. Пример разбиения на классы для иерархической системы

Пусть 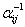- среднее время пребывания процесса в состоянии (i, j), a 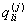- вероятность перехода из состояния (l, j - 1)в состояние (i, j), т.е. из состояния l класса j -1 в состояние i класса j.

Обозначим P_{i , j} (t)-вероятность того, что до момента t не было попадания в Q и в момент t процесс находился в состоянии i класса j. Тогда вместо системы (4.1) получаем

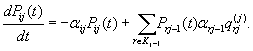(4.20)

С начальным условием Р ₁₁ (0)= 1, Р _ij (0) = 0, ij ¹ 1. Мы считаем, что класс К ₁состоит из одного состояния и движение начинается из него.

Система (4.20) может быть решена последовательно, так как справедлива рекуррентная формула

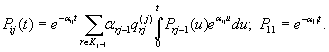(4.21)

С самого начала мы знаем вероятность P ₁₁ (t),затем по формуле (4.21) находим вероятности состояний второго класса, потом третьего, пока не переберем все классы. Функция надежности в этом случае может быть оценена следующей зависимостью

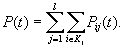(4.22)

Формула (4.21) показывает также,что P (t)будет представлять линейную комбинацию экспонент.

Отметим также, что для объектов описанного рода можно рассматривать a _ij как функции от t, что значительно расширяет круг приложений этой модели.

Значительно упрощается для данных моделей и вычисление среднего времени достижения критического множества,т.е. времени безаварийной эксплуатации. Пусть m (i, j)-среднее время достижения критического множества из состояния i класса j. Тогда

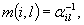(4.23)

где l - номер последнего класса. Для других классов имеем рекуррентное соотношение

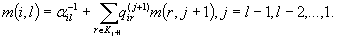(4.24)

Формулы (4.23) и (4.24)позволяют последовательно вычислить m (i, j). Пример 1 превращается в иерархическую модель,если b ₂ = 0, т.е. имеет граф переходов (рис. 4.16).

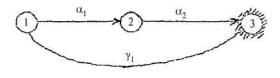
Рис. 4.16. Граф переходов для иерархических систем

В этой простейшей модели имеются два класса К ₁и К ₂,каждый из которых содержит по одному состоянию. Тогда

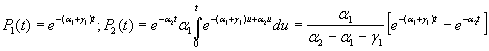(4.25)

и надежность системы

P (t)= P ₁ (t) + P ₂ (t). (4.26)

Среднее время достижения критического множества из состояния i

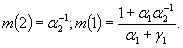
Иерархическая модель позволяет получить оценки для среднего времени достижения уровня и в более сложных случаях, когда имеются системы с регенерацией. Мы знаем, что для оценки этого времени необходимо знание двух чисел: t - среднее время периода регенерации и q - вероятность достижения критического множества на периоде регенерации.

Первое из этих чисел обычно нетрудно найти. Вся проблема во втором. В ряде математических работ ясно и наглядно показано, что основной вклад в q вносят так называемые монотонные траектории,грубо говоря, траектории без петель. Но это и означает иерархичность системы.Более подробно с этим методом можно познакомиться в указанной литературе. Мы же продемонстрируем его применение на следующих примерах.

Система с графом переходов (рис.4.17). Здесь q удается найти в явном виде

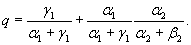(4.26)

Более сложная система с графом переходов (рис. 4.18). Точки регенерации - моменты возвращения в первое состояние.

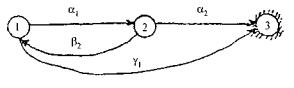
Рис. 4.17. Граф переходов из состояния для примера 4

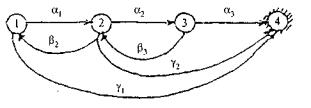
Рис. 4.18. Граф переходов из состояния для примера 5

В качестве оценки для q берем траектории, не имеющие петель.Перечислим их:

1 ®4, 1 ®2 ® 4, 1 ®2 ® 3 ®4.
I II III

Вероятности этих траекторий

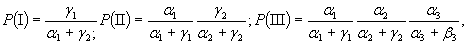
так что

q» P (I) + P (II) + P (III). (4.28)

На самом деле есть еще траектория типа 1 ® 2 ® 3 ® 4, но ее вероятность существенно меньше вероятностей уже указанных траекторий.

Результаты аналитических исследований позволили по-новому подойти к оценке надежности зданий за период длительной эксплуатации. При этом здание рассматривается как сложная взаимосвязанная система. Рассмотренные математические модели могут использоваться не только для прогнозирования надежности зданий в период эксплуатации, но и в случаях, когда требуется осуществить комплекс реконструктивных работ различной степени сложности. Установлены способы оценки входящих в модели параметров, которые преимущественно базируются на результатах статистической обработки наблюдений в сочетании с методами строительной механики и теории случайных процессов.

Установлены области рационального применения исследуемых моделей с учетом старения материала конструктивных элементов, наличия восстановленных свойств объекта после ремонтов с постоянно ухудшающимися свойствами конструктивных элементов и т.п.

Методический подход к оценке функции надежности представлен материалами в таблице 4.1.

Таблица 4.1

Методики оценки функции надежности P (t)реконструированных зданий

Предположения	Модели и методы	Способы оценки входящих в модель параметров
I. Предложение экспоненциальности распределения всех случайных величин	1. Цепь Маркова. Метод дифференциальных уравнений	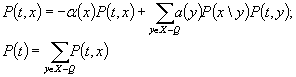1. Статистическая обработка результатов наблюдений за аналогичными объектами. 2. Методы строительной механики в сочетании с теорией случайных процессов
II. Учет старения элементов в предположении экспоненциальности	2. Цепь Маркова с параметрами, зависящими от времени. Метод дифференциальных уравнений	1. Статистическая обработка результатов наблюдений за аналогичными объектами. 2. Методы строительной механики в сочетании с теорией случайных процессов. 3. Метод наименьших квадратов
III. Наличие восстановленных свойств объекта после ремонтов. Малая вероятность аварии между ремонтами	Модель - регенерирующий процесс. Асимметрические методы	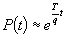1. Оценка среднего времени эксплуатации объекта по наблюдениям за однотипными объектами. 2. Оценка среднего времени до аварии с помощью алгебраических уравнений. 3. Метод наиболее вероятностных траекторий
IV. Движение только по монотонным траекториям, т.е. нет регенерации, свойства объекта постоянно ухудшаются	Иерархическая модель. Рекуррентная формула для вычисления вероятностей состояния	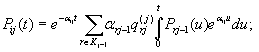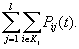1. Статистическая обработка результатов наблюдений за аналогичными объектами. 2. Методы строительной механики в сочетании с теорией случайных процессов. 3. Метод средних значений с помощью решения системы алгебраических уравнений

Она включает:

раздел предположений, которые позволяют учитывать различный характер случайных величин воздействия и изменения свойств реконструируемого объекта;

математические модели и методы,приемлемые для каждого конкретного случая; способы оценки входящих в модель параметров.

Как будет показано ниже,исследованные модели и методы решения адекватно описывают процессы снижения надежности систем как в период длительной эксплуатации, так и после проведения восстановительных работ (реконструкции).