Вопрос 40. Модель стабильного населения.
НО
•Это справедливо только для населений, режим воспроизводства которых (и возрастная структура) не меняются.
R0часто неверно интерпретируют как меру замещения материнского поколения дочерним в реальном населении
Эффективность воспроизводства или
«Цена простого воспроизводства» - мера экономичности воспроизводства населения
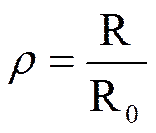 |
Сколько девочек в среднем необходимо родить женщине при данных уровнях возрастной рождаемости и смертности, чтобы обеспечить простое замещение материнского поколения дочерним?
Истинный коэффициент естественного прироста (коэффициент Лотки).
Альфред Лотка доказал, что каждому набору возрастных коэффициентов рождаемости и смертности закрытого однополого населения соответствует только один коэффициент естественного прироста, и, следовательно, только одно стабильное население.
Лотка вычислил Истинный коэффициент естественного прироста, решая следующее уравнение:
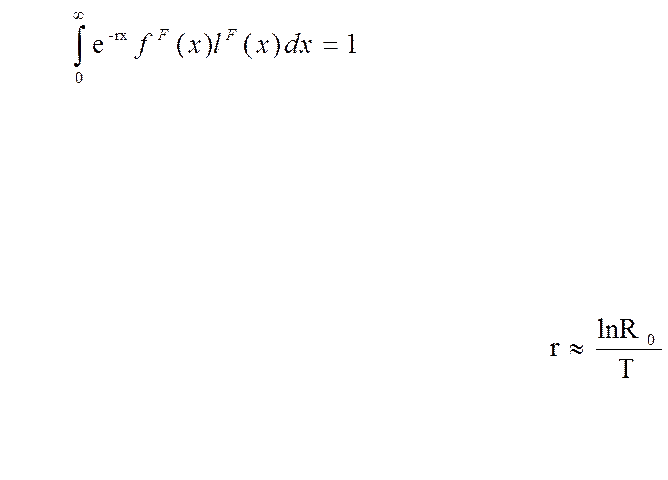
Упрощено: где T – длина поколения
Stabilis (лат.) – «постоянный, неизменный, устойчивый
Стабильное население – теоретическое закрытое население с неизменным во времени возрастными интенсивностями рождаемости и смертности, неизменной возрастной структурой.
Упрощённое изображение реальных взаимосвязей демографических процессов и возрастной структуры населения, позволяет анализировать закономерности воспроизводства населения при различных гипотезах естественного прироста.
История разработки модели стабильного населения:
1677 англ. актуарий М. Хейл высказал идею экспоненциального роста населения как основы стабильного населения
1760 Л.Эйлер:
«если в населении режим смертности неизменен, а число родившихся меняется по экспоненциальному закону, то возрастная структура неизменна»
1907 - 1948 А. Лотка обосновал основные положения теории стабильного населения для женского населения.
Неизменный коэффициент естественного прироста
.
Численность населения меняется по экспоненте
.
Числа родившихся и умерших меняются по экспоненте
.
Возрастная структура неизменна и зависит от 1) l(x) 2) r
Каждому сочетанию режима рождаемости и порядка вымирания соответствует единственное стабильное население.
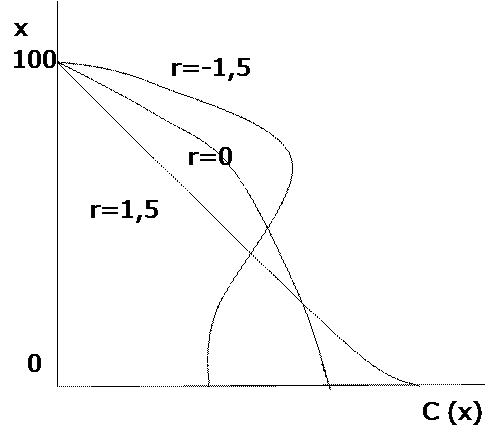
Возрастные пирамиды стабильного населения при разных коэффициентах естественного прироста и одной и той же функции дожития.
Свойство эргодичности стабильного населения (от лат. érgon - работа, hodós – путь)
Влияние прошлой возрастной структуры населения на последующую со временем постепенно ослабевает, и возрастная структура становится зависящей от режима воспроизводства в предшествующий период.
Сильная эргодичность (А.Лотка):
Если в реальном населении с определенного момента установятся неизменные интенсивности рождаемости и смертности, то в нем через некоторое время установится и неизменная возрастная структура, не зависящая от исходной формы возрастной пирамиды.
(Э. Коул, А. Лопес), конец 1950-х гг.
Свойство слабой эргодичности
Под влиянием непрерывно меняющихся рождаемости и смертности с каждым годом влияние исходной возрастной структуры на форму новой структуры ослабевает.
Любое население постепенно удаляется от своей возрастной структуры далекого прошлого.
Демографическая амортизация – автоматическое сглаживание колебаний общих коэффициентов и деформаций возрастной структуры.
Приложения модели стабильного населения:
•Основа для расчёта интегральных характеристик режима воспроизводства населения: истинный коэффициент естественного прироста, нетто и брутто-коэффициенты воспроизводства
•Исследование теоретических проблем, изучение которых на основе наблюдений за реальными данными затруднено. В первую очередь – изучение взаимосвязей между возрастной структурой и процессами смертности и рождаемости
•Применяется в демографических расчётах и прогнозах при отсутствии достоверных статистических данных о населении (применительно к населению с относительно неизменным режимом воспроизводства)
•Для решения прикладных задач: в актуарных расчетах, для изучения взаимосвязи демографического и экономического роста, для изучения влияния возрастной структуры на развитие социально-экономических процессов и др.
 2013-12-31
2013-12-31 846
846








