Вопрос 41. Модель стационарного населения

Stationarius (лат.) – «неподвижный», т.к. все демографические параметры не меняются со временем.

Стационарное население – теоретическое закрытое население с неизменными:
- абсолютными числами рождений и смертей, - численностью населения,
- возрастной структурой
- возрастными характеристиками смертности, задаваемыми таблицей смертности.

Другой взгляд на таблицу смертности…

История разработки модели стационарного населения:

1680 Лейбниц – идея стационарного населения: «Рождаемость людей всегда остается постоянной и настолько равна смертности, что общая численность людей практически не меняется, и даже число людей в каждом возрасте остается неизменным»

1693 Э. Галлей – реализация идеи СН в работе «Оценка смертности человека на основе старых таблиц рождений и отпеваний г. Бреслау с попыткой рассчитать пожизненную ренту»:

- разработка метода смертных списков

- гипотеза закрытого населения: «изучение смертности требует, чтобы по возможности те люди, которых мы изучаем, не мигрировали и умирали там, где рождены, т.е. чтобы не было ни роста населения за счет иммиграции, ни убыли за счет эмиграции»

XIX в. Г. Кнапп: разработка количественных соотношений стационарного населения.

Свойства стационарного населения:

Из равенства числа умерших числу родившихся следует:

1. Равенство общих коэффициентов рождаемости и смертности
n = m = 1/E(0)

2. Неизменность во времени общей численности населения

А также:

3.Возрастные характеристики реального и условного поколений идентичны

В том числе средний возраст умерших равен ожидаемой продолжительности предстоящей жизни при рождении

В реальном населении: меняются из года в год все параметры (численность населения, числа родившихся и умерших, возрастная структура)

Применение модели стационарного населения:

•В качестве стандарта при сравнительном анализе демографических процессов в разных населениях.

•Метод смертных списков для построения таблиц смертности в палеодемографических исследованиях (Р. Пресса: «хотя соответствие между реальным населением и теоретическим стационарным населением никогда не может быть вполне строгим, все же в некоторых случаях такое сопоставление, поскольку оно допустимо, может дать некоторые полезные сведения»)

•В основе долгосрочных прогнозов ООН лежит гипотеза стационарности

•В недемографических исследованиях

Модель стационарного населения расширяет круг приложений таблиц смертности за пределы изучения смертности. С помощью модели стационарного населения могут решаться не только демографические, но и самые разнообразные экономические задачи, такие как, например, анализ движения кадров на предприятии, особенности формирования автомобильного парка города, планирование расходов в области социального обеспечения. Все эти задачи объединяет то, что, во-первых, подлежащие изучению совокупности состоят из элементов, которые выбывают из них через определенное время и, следовательно, обладают такой характеристикой, как продолжительность жизни в данной совокупности. Во-вторых, количество этих элементов и их распределение по возрасту предполагается неизменным или почти неизменным во времени. Разработанные более трех столетий тому назад таблицы смертности превратились из чисто демографического в один из общенаучных методов исследования.

из его определения:

1) из равенства числа умерших числу родившихся, т.е. 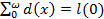, следует:

а) естественный прирост стационарного населения равен нулю;

б) общие коэффициенты рождаемости и смертности в стационарном населении равны: m = n;

в) (с учетом условия закрытости) общая численность стационарного

населения неизменна во времени.

2) общие коэффициенты смертности и рождаемости обратно пропорциональны ожидаемой продолжительности предстоящей жизни при рождении. Из определения ожидаемой продолжительности предстоящей жизни при рождении e(0)=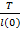и определений общих коэффициентов следует n=m=.

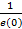3) постоянство всех демографических показателей обусловливает идентичность всех возрастных характеристик реального и условного поколений в стационарном населении, что хорошо видно на сетке Лексиса.

4) численность поколений в стационарном населении равна числу родившихся, умноженному на среднюю продолжительность предстоящей жизни при рождении, т.е. = e(0) ⋅ l(0). Это свойство вытекает из определения ожидаемой продолжительности жизни и интерпретации функции T (x) в модели стационарного населения.

5) средний возраст умерших стационарного населения равен ожидаемой продолжительности предстоящей жизни при рождении. Это свойство непосредственно вытекает из определения соответствующих показателей в таблицах смертности:

e(0)=,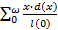

где x - средний возраст в интервале (x, x+1)

Средний возраст умерших в реальном населении отличается от ожидаемой продолжительности предстоящей жизни, поскольку он аккумулирует в себе колебания чисел родившихся и особенности возрастной структуры умерших, отличающейся от структуры умерших в стационарном населении.