Ротационная динамика

В ДЕМОГРАФИИ

МАТЕМАТИЧЕСКИЕ МОДЕЛИ

МАТЕРИАЛЫ ДЛЯ ИЗУЧЕНИЯ ДИСЦИПЛИНЫ

Составитель П. А. Ватник

Санкт-Петербург

СОДЕРЖАНИЕ

1. Ротационная динамика

2. Продольный анализ

3. Некоторые аналитические функции дожития

4. Дискретная модель дожития

5. Модель воспроизводства стабильного населения

6. Доля трудоспособного населения

7. Модели генетической демографии

8. Модели эпидемий

9. Модели миграции

Баланс запаса и потоков:

X ′= x ₊ – x _–, (1)

где X — объем запаса, X ′= dX/dt, x ₊ и x _– — интенсивности потоков, индексы «+» и «–» обозначают, что величина относится к входному или выходному потоку соответственно.

Допустим, что X обозначает объем запаса, а Y – его массу. Масса также отвечает балансовому условию вида (1):

Y ′ = y ₊ – y _–. (2)

Оба соотношения предполагают, что в запасе отсутствует порождение/исчезновение объема и массы, и вся динамика определяется только входом и выходом (иначе: динамика имеет целиком экзогенную природу). Порождение или исчезновение потребовали бы дополнительного слагаемого в правой части.

Пусть r обозначает среднюю плотность запаса, r₊, r_– — плотности соответствующих потоков, так что

Y = r X; y ₊ = r₊ x ₊; y _– = r_– x _– .

Подставляя эти выражения в (2), имеем:

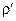X + r X ′ = r₊ x ₊ – r_– x _– ,

или, принимая во внимание (1),

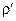X + r x ₊ – r x _– = r₊ x ₊ – r_– x _– .

Перегруппировав слагаемые, получим дифференциальное уравнение динамики средней плотности запаса:

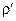X = (r₊ – r) x ₊ – (r_– – r) x _– .

Разделив обе части на X и используя обозначения r ₊ = x ₊ /X для оборачиваемости по входу и r _– = x _– /X для оборачиваемости по выходу, получим уравнение, связывающее плотности потоков с оборачиваемостью запаса:

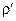= (r₊ – r) r ₊ – (r_–– r) r _–. (3)

Здесь мы считали, что изменение средней плотности обусловлено только ротацией. Если это не так, то можно считать, что в запасе происходит порождение (положительное или отрицательное) массы без изменения объема. В частности, если скорость a этого процесса на единицу объема запаса постоянна, то в правой части (2) появляется дополнительно слагаемое a X, а в правой части (3) — слагаемое a:

Y ′ = y ₊ – y _– + a X; (2a)

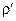= (r₊ – r) r ₊ – (r_–– r) r _– + a. (3a)

Случай a = 0 уже рассмотрен. Другое интересное частное значение: a = 1 — имеет место при описании динамики возраста, стажа, продолжительности пребывания в некотором состоянии и т. п.

Применительно к демографии уравнения (2а) и (3а) описывают, в частности, связь характеристик рождаемости, смертности, старения населения. Пусть X — численность населения, r — средний возраст, Y — «возрастная масса», измеряемая в человеко-годах. Входной поток — поток рождений, выходной — поток смертей, так что r ₊ и r _– —коэффициенты рождаемости и смертности соответственно; r₊ = 0, r_– — средний возраст умерших. Так как каждый живущий за год становится старше на год, эндогенный рост возрастной массы идет со скоростью X, так что a = 1, и уравнение (3a) для возрастной динамики принимает вид

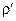= 1 – r r ₊ – (r_– – r) r _– . (4)

Имея в виду, что r ₊ – r _– = b — темп прироста численности населения, равенство (4) можно также представить в виде:

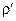= 1 – r_– r _– – br

Для стабильного населения (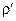= 0):

r r ₊ + (r_– – r) r _– = 1

или

r– r – + br= 1.

(5)

В качестве иллюстрации рассмотрим стабильное население, средний возраст которого r = 30 лет, рождаемость r ₊ = 0.02 г ^–1, смертность r _– = 0.008 г ^–1, так что темп прироста населения b= 0.02 – 0.008= 0.012 г ^–1. Из равенства (5), принимающего конкретный вид 0.008r_– + 0.012 · 30 = 1, находим: r_– = 80 лет.