Основные соотношения. Функция дожития и повозрастная смертность связаны соотношениями
V (t) = 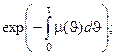 m(t) = –
m(t) = –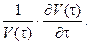
Средняя продолжительность жизни
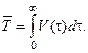
Ожидаемая продолжительность предстоящей жизни лиц в возрасте t:
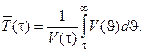
Доля лиц в диапазоне возрастов [t1, t2] в общей численности (для стационарного населения)
w (t1, t2) = 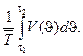
В дальнейшем будет использовано обозначение
I (t1, t2) = 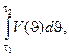
так что
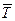 = I (0, ∞);
= I (0, ∞); 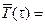 I (t,∞) /V (t); w (t1, t2) = I (t1, t2) /
I (t,∞) /V (t); w (t1, t2) = I (t1, t2) / 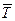 .
.
Модель нестареющего населения. Характеризуется постоянством повозрастной смертности:
m(t) = m = const, 0 £ t < ∞.
Отсюда — функция дожития
V (t) = e– mt, 0 £ t < ∞.
Средняя продолжительность жизни 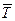 = 1 / m. Ожидаемая продолжительность предстоящей жизни лиц в возрасте t:
= 1 / m. Ожидаемая продолжительность предстоящей жизни лиц в возрасте t: 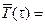 1 / m.
1 / m.
Доля лиц в диапазоне возрастов [t1, t2] в общей численности (для стационарного населения) w (t1, t2) = 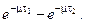
Модель мгновенно стареющего населения. Характеризуется постоянством повозрастной смертности в пределах от 0 до максимального возраста T:
m(t) = m = const, 0 £ t < T.
Значению t = T соответствует отрицательная d-образная компонента, так что функция дожития обращается в 0 при t ³ T:
V (t) = e– mt, 0 £ t < T.
В этом случае
I (t1, t2) = (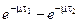 ) / m.
) / m.
Остальные характеристики:
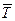 =
=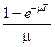 ;
; 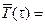 [1 – e m( T – t)] / m; w (t1, t2) =
[1 – e m( T – t)] / m; w (t1, t2) = 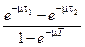 .
.
Степенная модель. Как и в предыдущем случае, возраст ограничен сверху предельным значением T; повозрастная смертность описывается выражением
m(t) =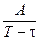 , 0 £ t < T, A > 0.
, 0 £ t < T, A > 0.
Теперь функция дожития имеет вид
V (t) = 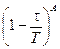 ,
,
а интеграл от нее —
I (t1, t2) =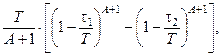
так что
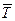 =
=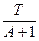 ;
; 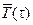 =
= 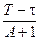 ; w (t1, t2) =
; w (t1, t2) =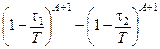 .
.
Удобство данной функции для различных упражнений состоит в том, что параметр A просто выражается через T и 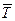 :
:
A = 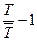 .
.
Гиперболическая модель. Здесь также возраст ограничен сверху предельным значением T; функция дожития
V (t) = 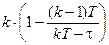
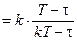 , 0 £ t < T, k > 1.
, 0 £ t < T, k > 1.
Ей соответствует повозрастная смертность
m(t) = 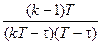
и интеграл
I (t1, t2) = 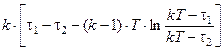 .
.
Остальные характеристики:
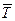 =
=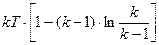 ;
;
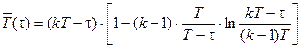 .
.
 2013-12-31
2013-12-31 725
725







