Постановка задачи

В ПОПУТНОМ НАПРАВЛЕНИИ

МЕТОД ОПРЕДЕЛЕНИЯ МИНИМАЛЬНО-БЕЗОПАСНОГО РАССТОЯНИЯ (ДИСТАНЦИИ) МЕЖДУ АВТОМОБИЛЯМИ, ДВИЖУЩИМИСЯ

Существующая методика определения минимально-безопасного расстояния между автомобилями, движущимися в попутном направлении, не отражает всю полноту процесса изменения этого расстояния в зависимости от изменения параметров движения автомобилей и их технического состояния. Формулы 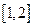, предлагаемые для определения минимально-безопасного расстояния между автомобилями, охватывают не все случаи соотношения параметров их движения и параметров, характеризующих их техническое состояние. Поэтому эти формулы не всегда применимы. Предлагаемый метод позволяет последовательно исследовать изменение минимально-безопасного расстояния (дистанции) между автомобилями в зависимости от изменения параметров их движения.

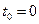Рассмотрим прямолинейное поступательное движение автомобилей и , причем автомобиль движется сзади автомобиля . Будем считать, что в начальный момент времени расстояние между автомобилями и равно 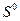, а скорости соответственно равны 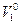и .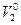

Так как при поступательном движении все точки каждого из автомобилей двигаются по конгруэнтным траекториям, имеют равные скорости и ускорения, то мы можем рассматривать движение автомобиля как движение средней точки его переднего бампера, а движение автомобиля как движение средней точки его заднего бампера. В этом случае в общем виде движение автомобилей и на отрезке времени описывается системами дифференциальных уравнений:

для автомобиля

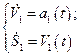(2.1.1)

с начальными условиями

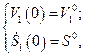(2.1.2)

для автомобиля

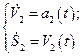(2.1.3)

с начальными условиями

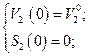(2.1.4)

где 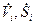- означают производные по времени;

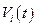- скорость 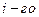(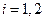) автомобиля в момент времени ;

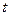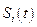- путь, пройденный 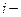м автомобилем к моменту времени ;

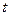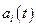- ускорение 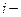го автомобиля в момент времени ;

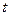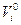- скорость 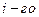(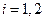) автомобиля в начальный момент времени ;

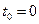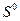- расстояние между автомобилями и в начальный момент време-ни .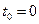

Будем предполагать, что функции 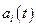(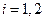) на отрезке времени 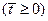являются кусочно-непрерывными функциями, допускающими конечное число точек разрыва первого рода. Это обеспечивает непрерывность и дифференцируемость функци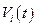й и 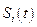на этом отрезке времени.

Решение системы (2.1.1) с начальными условиями (2.1.2) имеет вид

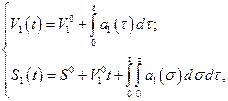(2.1.5)

а решение системы (2.1.3) с начальными условиями (2.1.4) может быть записано в виде

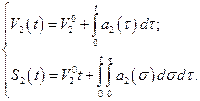(2.1.6)

Используя равенства (2.1.5), (2.1.6), запишем выражения функци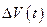й и 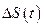, которые определяются равенствами

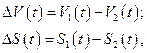(2.1.7)

получим

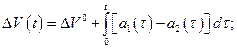(2.1.8)

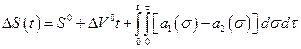, (2.1.9)

где .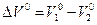

Отметим, что равенство (2.1.9) может быть записано в виде

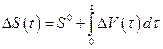, (2.1.10)

где 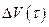определено первым равенством в (2.1.7). Нетрудно видеть, что если функции 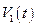, 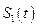являются решением системы (2.1.1) с начальными условиями (2.1.2), а функции 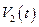и 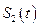являются решением системы (2.1.3) с начальными условиями (2.1.4), то функци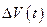и и 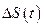являются решением системы дифференциальных уравнений

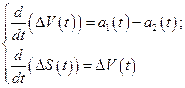(2.1.11)

с начальными условиями

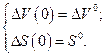(2.1.12)

Из равенства (2.1.10) видно, что функция 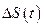может быть представлена в виде

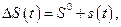(2.1.13)

где

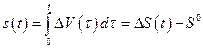. (2.1.14)

Очевидно, что если функци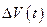и и 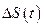являются решением системы дифференциальных уравнений (2.1.11), то в этом случае функци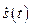и и 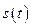есть решение системы (2.1.11) с начальными условиями

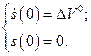
Равенство (2.1.13) показывает, что исследование на экстремум функции 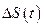может быть сведено к исследованию на экстремум функции 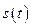, которая определена равенством (2.1.14), так как они отличаются на постоянную величину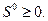

При движении автомобилей в рассматриваемом случае водитель автомобиля может выбирать режим движения своего автомобиля в соответствии с правилами дорожного движения и дорожной обстановкой. Водитель же автомобиля вынужден выбирать такое расстояние между автомобилями (учитывая обстановку на дороге), чтобы, соблюдая правила дорожного движения, не допустить столкновения с впереди движущимся автомобилем в любой момент времени. Это означает, что водитель автомобиля стремится к тому, чтобы расстояние между автомобилями 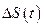в любой момент времени было больше нуля, т. е.

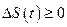. (2.1.15)

Постановка задачи. Пусть движение автомобилей и на отрезке времени описывается системами дифференциальных уравнений (2.1.1), (2.1.3) с начальными условиями (2.1.2), (2.1.4) соответственно. Необходимо выбрать такое минимальное начальное расстояние 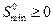между автомобилями в начальный момент времени 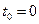, чтобы для любых 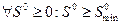неравенство (2.1.15) выполнялось для всех 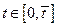, а для 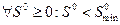на отрезке времени необходимо найдется момент времени 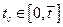, при котором произойдет столкновение автомобилей и .