Модель движения автомобиля при экстренном торможении (юзом) и определение длины остановочного пути

ПРИ ЭКСТРЕННОМ ТОРМОЖЕНИИ

В качестве модели движения автомобиля при экстренном торможении в литературе по дорожно-транспортной экспертизе в неявном виде чаще всего используется следующая модель.

Прямолинейное поступательное движение автомобиля при экстренном торможении на отрезке времени может быть описано системой дифференциальных уравнений

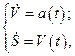(1.1.1)

с начальными условиями

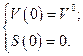(1.1.2)

В системе уравнений (1.1.1) функция 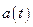определяется равенством

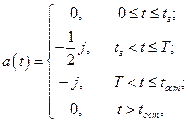(1.1.3)

где 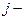замедление автомобиля ;

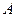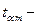время движения автомобиля 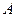до полной остановки, которое определяется позже.

Величина 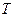в (1.1.1) определяется равенством

,

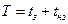где 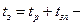время запаздывания;

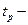время реакции водителя;

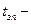время запаздывания тормозного привода;

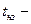время нарастания замедления.

График функции 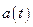изображен на рис.1.1.1.

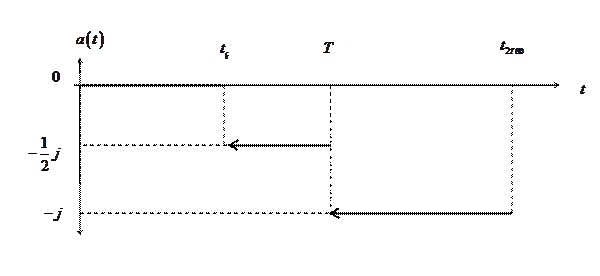
Рис. 1.1.1

Решение системы (1.1.1) с начальными условиями (1.1.2) с учетом равенства (1.1.3) имеет вид

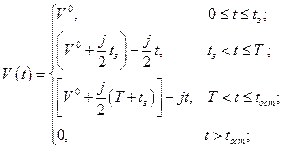(1.1.4)

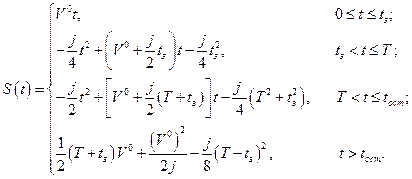(1.1.5)

Время движения автомобиля до полной остановки 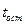определяется из условия 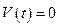. Из равенств (2.1.4) видно, что автомобиль 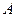может остановиться в двух случаях.

Случай 1. На полуинтервале 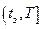в момент времени

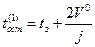, (1.1.6)

если выполняется неравенство

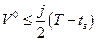. (1.1.7)

Остановочный путь в этом случае определяется равенством

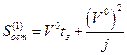. (1.1.8)

Механический смысл этого момента остановки 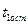состоит в том, что автомобиль , имея незначительную скорость, может остановиться во время нарастания замедления.

Случай 2. В момент времени

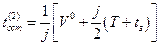, (1.1.9)

если выполняется неравенство

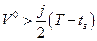. (1.1.10)

Очевидно, что 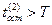, так как в силу неравенства (1.1.10) имеем

.

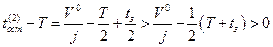Остановочный путь в этом случае равен

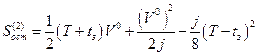. (1.1.11)

Если считать, что обычно и делают, что величина

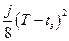
мала, то, отбрасывая в равенстве (1.1.10) член второго порядка малости 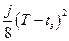, получим

.

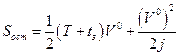Эта формула может быть записана в виде

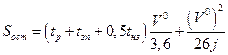. (1.1.12)

Последняя формула совпадает с соответствующей формулой в 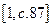. Этой формулой обычно и пользуются при определении остановочного пути автомобиля.

Равенства (1.1.8) и (1.1.11), с учётом неравенств (1.1.7) и (1.1.10), дают возможность записать выражение длины остановочного пути в общем виде

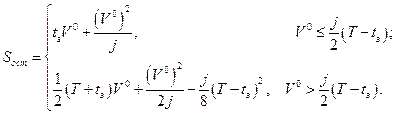(1.1.13)

Равенство (1.1.13) показывает, что вычисление остановочного пути по формулам (1.1.11), (1.1.12) может привести к значительной погрешности при определении остановочного пути в рамках рассматриваемой модели движения, когда транспортное средство движется с небольшой скоростью и когда время нарастания замедления велико. Кроме того, равенства (1.1.13) показывают, что остановочный путь автомобиля существенно зависит от его технического состояния, в частности, от продолжительности времени нарастания замедления. Для точного определения остановочного пути необходимо проводить замеры времени нарастания замедления на каждом конкретном автомобиле в конкретных условиях. Следует отметить, что время нарастания замедления зависит не только от технического состояния автомобиля, но и от погодных и дорожных условий.

Рассмотрим примеры.

Пример 1. Пусть исправное грузопассажирское транспортное средство, изготовленно до 01.01.81. Величину замедления 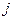ТС, время запаздывания тормозного привода 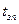и время нарастания замедления 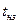возьмем из таблицы П.8 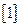: 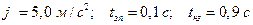. Время реакции водителя 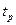будем считать равным 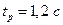. Необходимо найти длину остановочного пути, если ТС двигалось со скоростью:

А)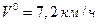

Определим величину

.

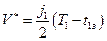В рассматриваемом случае эта величина равна 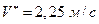. Так как

,

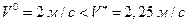то для определения остановочного пути необходимо пользоваться первым равенством в (1.1.7). Подставляя в первое равенство (1.1.13) исходные значения и произведя вычисления, получим

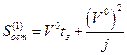
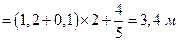. (1.1.14)

Теперь вычислим длину остановочного пути по формуле (1.1.12):

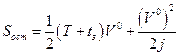
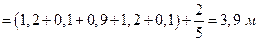. (1.1.15)

Сравнивая результаты вычислений (1.1.14) и (1.1.15), видим, что разница в определении остановочного пути составляет 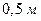. При такой скорости разница в длине остановочного пути является существенной.

В)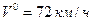

В рассматриваемом случае выполняется неравенство

,

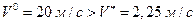следовательно, остановочный путь ТС необходимо вычислять, используя формулу (1.1.11):

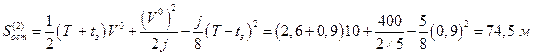. (1.1.16)

Теперь вычислим остановочный путь по второй формуле (1.1.12). Получим

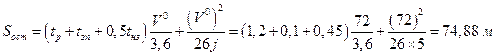. (1.1.17)

Сравнивая результаты (1.1.16) и (1.1.17), видим, что .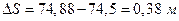

Картина совершенно меняется, когда транспортное средство имеет неисправную тормозную систему, вызывающую рост 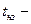времени нарастания замедления.

Пример 2. Пусть в вследствие неисправности главного тормозного цилиндра ТС, рассматриваемого в примере 1, время нарастания замедления 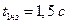. Тогда величина 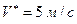, что соответствует скорости 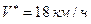. Вычислим остановочный путь, если ТС двигалось со скоростью:

А)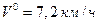

Сначала определим длину остановочного пути по формуле (1.1.12):

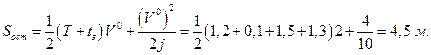
Теперь определим длину остановочного пути по первой формуле (1.1.13), так как выполняется неравенство

.

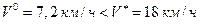Получим

.

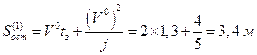В этом случае .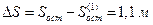

В) .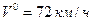

Определим остановочный путь по формуле (1.1.12)

.

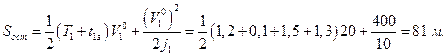Теперь определим длину остановочного пути по второй формуле (1.1.13), так как

>.

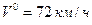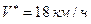Получим

.

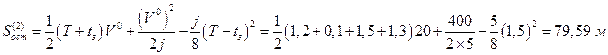То есть остановочный путь, вычисленный по формуле (1.1.12), на 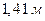длиннее остановочного пути, который вычислен по второй формуле (1.1.13).

Пример 3. Рассмотрим теперь в качестве примера движение автомобиля BMW серий 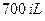. Параметры торможения автомобиля возьмем из таблицы П.11 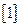: 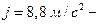установившееся замедление; 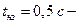время нарастания замедления. Возьмем время реакции водителя 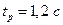; время запаздывания тормозного привода .

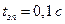А) Вычислим остановочный путь автомобиля при заданных параметрах торможения при начальной скорости автомобиля 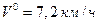по формулам (1.1.12) и (1.1.13).

Определим величину

.

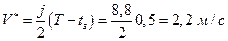Так как выполняется неравенство

,

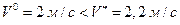то воспользуемся первой формулой (1.1.13).

.

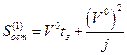
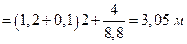Теперь вычислим остановочный путь по формуле (1.1.12)

.

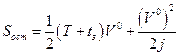
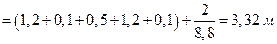Разность результатов составит

.

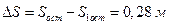В) Пусть скорость автомобиля равна 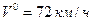, тогда выполняется неравенство

.

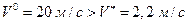Длина остановочного пути, вычисленного по второй формуле (1.1.13) составит

.

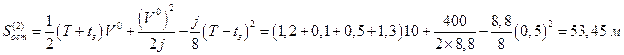Длина остановочного пути, вычисленного по формуле (1.1.12), составит

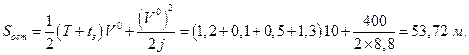
Величина .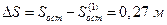

Пример 4. Пусть в результате или неисправности тормозной системы или мокрых тормозных дисков время нарастания замедления 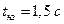. Вычислим остановочный путь автомобиля BMW при начальных скоростях: А) 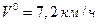; В) 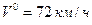, используя формулы (1.1.12) и (1.1.13).

А) .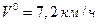

Вычислим в рассматриваемом случае величину

.

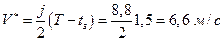Длина остановочного пути, вычисленного по формуле (1.1.12), равна

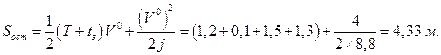
Длина остановочного пути, вычисленного по первой формуле (1.1.13), так как выполняется неравенство

,

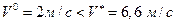равна

,

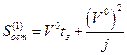
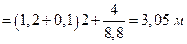тогда .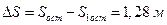

В) .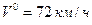

Длина остановочного пути, вычисленного по формуле (1.1.12), равна

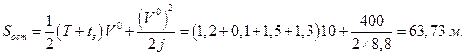
Длина остановочного пути, вычисленного по второй формуле (1.1.13), равна

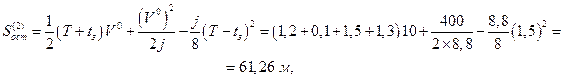
тогда .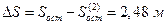

Приведенные примеры показывают, что для более точного определения длины остановочного пути при использовании данной модели необходимо пользоваться формулами (1.1.13). Кроме того, следует отметить, что длина остановочного пути линейно зависит от времени запаздывания тормозного привода автомобиля и нелинейно от продолжительности времени нарастания замедления 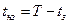и, следовательно, от технического состояния тормозной системы автомобиля.