Аналогично решаются и системы линейных дифференциальных уравнений с постоянными коэффициентами. Отличие будет лишь в том, что вместо одного операторного уравнения, получим систему таких уравнений, которые будут линейными относительно изображений искомых функций.
Пример № 2. Найти решение системы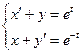 призаданных начальных условиях
призаданных начальных условиях 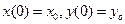 .
.
Решение.
Перейдем к изображениям: пусть 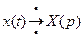
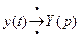 ,
,
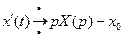 ,
, 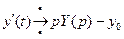 ,
,
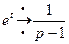 ,
, 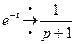 (по таблице изображений).
(по таблице изображений).
Подставим в заданную систему и получим систему из двух операторных уравнений:
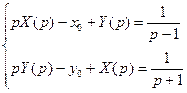
Из первого уравнения выразим 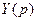
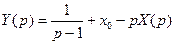 (*)
(*)
и подставим во второе уравнение: 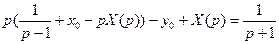 .
.
Выразим отсюда 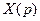 :
:
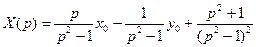 (**)
(**)
Подставим (**) в выражение (*):
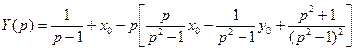
Преобразуем:
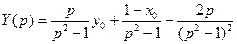 (***)
(***)
Найдем оригиналы для каждого слагаемого равенств (**) и (***) отдельно.
Рассмотрим (**). Преобразуем равенство к виду, пригодному для нахождения оригиналов.
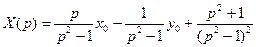
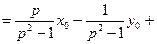
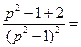
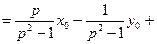
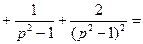
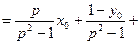
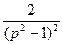
Найдем оригиналы:
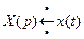 ,
, 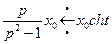 ,
, 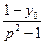
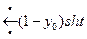 – по таблице изображений.
– по таблице изображений.
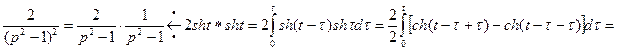
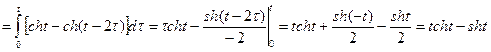 .
.
В данном случае воспользовались теоремой Бореля о свертке функций и следующими формулами для гиперболических функций: 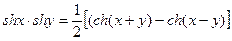 ,
, 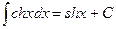
Следовательно, 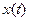 имеет вид:
имеет вид:
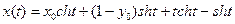
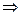
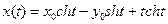
Рассмотрим (***).

Найдем оригиналы:
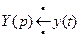 ,
, 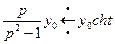 ,
, 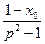
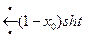 – по таблице изображений.
– по таблице изображений.
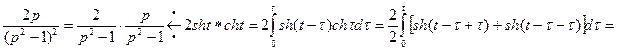
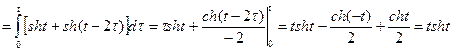
Воспользовались теоремой Бореля о свертке функций и следующими формулами для гиперболических функций: 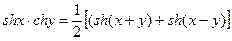 ,
, 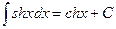 ,
, 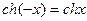 .
.
Следовательно, 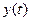 имеет вид:
имеет вид: 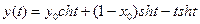
Ответ: Решение системы имеет вид: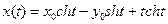
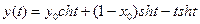
Замечание. 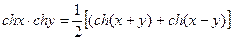
 2014-01-24
2014-01-24 703
703








