Теорема 5. (условие существование оригинала) Пусть функция F (p) комплексного переменного p = x + iy удовлетворяет следующим условиям:
1) F (p) – аналитическая функция в области 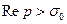 ,
,
2) в области 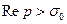
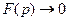 при
при 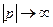 равномерно относительно arg p,
равномерно относительно arg p,
3) для всех 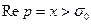 сходится интеграл
сходится интеграл 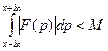 ,
,
тогда F (p) при 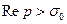 является изображением функции f (t) действительного переменного t, которая определяется выражением (8).
является изображением функции f (t) действительного переменного t, которая определяется выражением (8).
(без доказательства)
Во многих случаях интеграл Меллина может быть вычислен с помощью контурных интегралов от функции комплексного переменного. Но непосредственное применение формулы обращения часто затруднительно, поэтому пользуются теоремами разложения, являющимися следствиями теоремы 3.
Теорема 6. (вторая теорема разложнения). Если изображение F (p) является однозначной функцией и имеет лишь конечное число особых точек p 1, p 2, …, pn, лежащих в конечной части плоскости, то
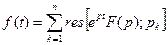 (9)
(9)
(без доказательства)
Теорема 6. (первая теорема разложнения, случай регулярной на бесконечности функции). Если функция F (p) аналитична в некоторой окрестности бесконечно удаленной точки 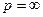 и ее разложение в ряд Лорана в окрестности точки
и ее разложение в ряд Лорана в окрестности точки 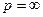 имеет вид
имеет вид
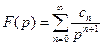 , (10)
, (10)
то функция
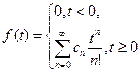 (11)
(11)
является оригиналом f (t) данной функции F (p).
(без доказательства)
Замечание. Еслиразложение аналитической функции F (p) в ряд Лорана в окрестности точки 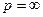 имеет вид
имеет вид
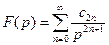 , (12)
, (12)
то ее оригиналом f (t) является функция
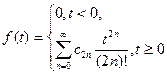 . (13)
. (13)
 2014-01-24
2014-01-24 1137
1137








