2014-01-24
713
Применение методов операционного исчисления.
В основном методы операционного исчисления используются для решения обыкновенных дифференциальных уравнений, уравнений в частных производных, краевых задач математической физики.
Из § 1 п.1 известно, что если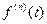 
удовлетворяет условиям существования изображения, то справедливы свойства: 
, 
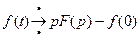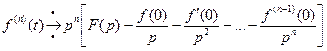. С помощью данного свойства задача Коши для обыкновенного дифференциального уравнения с постоянными коэффициентами сводится к простейшей алгебраической задаче для изображений.
Пусть дано обыкновенное дифференциальное уравнение с постоянными коэффициентами
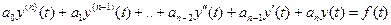
с заданными начальными условиями:
.
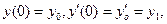
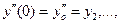
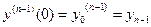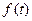задана при 
.
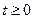Применим к обеим частям уравнения преобразование Лапласа, используя свойства:
, 
, 
, 
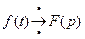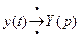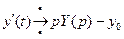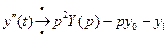и т.д.
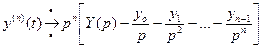
Подставим в 
уравнение:
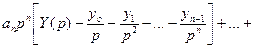
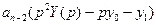
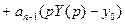
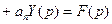
Получим операторное или алгебраическое уравнение относительно р.
Выразим отсюда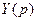 
. Приведем уравнение к виду, пригодному для нахождения оригиналов. Воспользуемся таблицами, свойствами изображений, теоремами разложения и перейдем к оригиналам, т.е найдем общее решение уравнения, затем частное решение, удовлетворяющее заданным начальным условиям.
Продемонстрируем вышесказанное на примере.
Пример № 1. Найти общее решение уравнения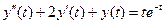 
, а также его частное решение, удовлетворяющее начальным условиям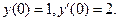 
Решение.
Перейдем к изображениям: пусть , , ,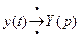 
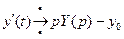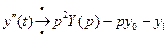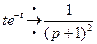(по таблице изображений).
Подставим в уравнение и получим операторное уравнение:
.
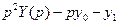
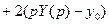
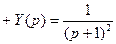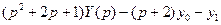
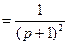
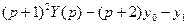
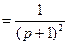
Выразим :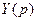
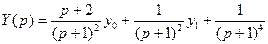
Приведем к виду, пригодному для нахождения оригиналов:
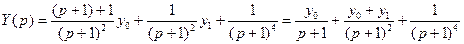
Найдем оригиналы для каждого слагаемого отдельно. Для этого пользуемся таблицей изображений.
, 
, 
, 
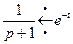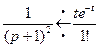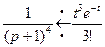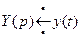
Подставим в уравнение (при этом применим свойство линейности) и найдем общее решение:
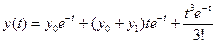
Обозначим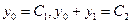 
. Запишем решение в виде:
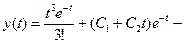общее решение уравнения.
Найдем частное решение, удовлетворяющее начальным условиям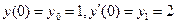 
из системы:
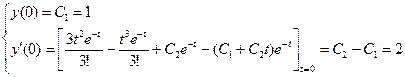
Отсюда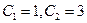 
, тогда
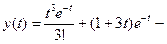частное решение уравнения.
Ответ: 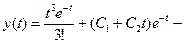общее решение, 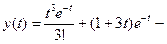частное решение уравнения.
