Примеры на использование теорем разложения.
Пример № 1. Найти оригинал функции 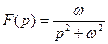 , где
, где 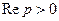 .
.
Условия теоремы 5 выполнены, следовательно, оригинал функции 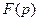 может быть найден по формуле Меллина. Функция
может быть найден по формуле Меллина. Функция 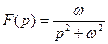 является аналитической, однозначной функцией и имеет две особые точки
является аналитической, однозначной функцией и имеет две особые точки 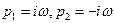 , так как знаменатель обращается в них в нуль:
, так как знаменатель обращается в них в нуль:
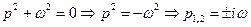 .
.
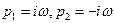 – полюсы 1-го порядка, т.к.
– полюсы 1-го порядка, т.к.
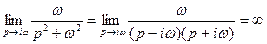 ,
, 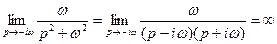
При 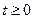 из 2-ой теоремы разложения следует, что
из 2-ой теоремы разложения следует, что
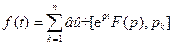
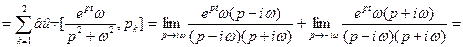
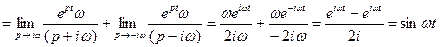
Ответ: 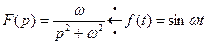
Пример № 2. Найти оригинал функции 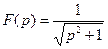 .
.
Решение.
Найдем особые точки: 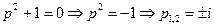 .
.
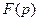 является однозначной, аналитической функцией в окрестности бесконечно удаленной точки
является однозначной, аналитической функцией в окрестности бесконечно удаленной точки 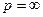 , значит, в этой окрестности
, значит, в этой окрестности 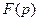 может быть разложена в ряд Лорана:
может быть разложена в ряд Лорана:
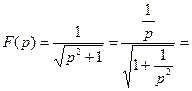
[ используем известное разложение в ряд Маклорена функции 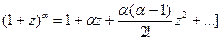
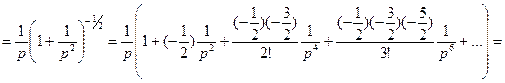
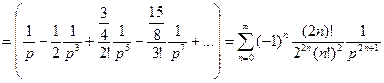 Из 1-ой теоремы разложения следует, что если
Из 1-ой теоремы разложения следует, что если 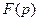 , аналитическая в некоторой окрестности т.
, аналитическая в некоторой окрестности т. 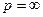 имеет разложение в ряд Лорана вида
имеет разложение в ряд Лорана вида 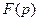
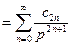 , то оригиналом ее является функция
, то оригиналом ее является функция 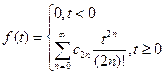 . В нашем случае
. В нашем случае 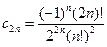 , следовательно
, следовательно
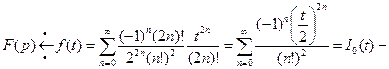 функция Бесселя нулевого порядка
функция Бесселя нулевого порядка
Ответ: 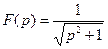
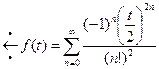
Пример № 3. Найти оригинал функции 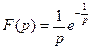 .
.
Решение.
1 способ (с использованием теоремы 1)
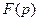 является однозначной, аналитической функцией в окрестности бесконечно удаленной точки
является однозначной, аналитической функцией в окрестности бесконечно удаленной точки 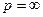 . Разложим ее в этой окрестности в ряд Лорана:
. Разложим ее в этой окрестности в ряд Лорана:
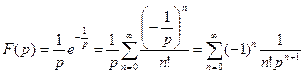
Из 1-ой теоремы разложения следует, что если 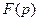 , аналитическая в некоторой окрестности т.
, аналитическая в некоторой окрестности т. 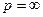 имеет разложение в ряд Лорана вида
имеет разложение в ряд Лорана вида 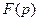
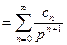 , то оригиналом ее является функция
, то оригиналом ее является функция 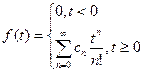 . В нашем случае
. В нашем случае 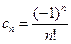 , следовательно
, следовательно
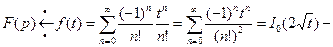 функция Бесселя первого порядка с нулевым индексом.
функция Бесселя первого порядка с нулевым индексом.
2 способ (с использованием теоремы 2)
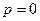 – существенно особая точка функции
– существенно особая точка функции 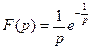 , так как
, так как 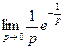 не существует, тогда по теореме 1
не существует, тогда по теореме 1 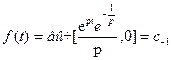 . Т.е. для решения задачи нам требуется найти коэффициент при (-1)–ой степени разложения функции
. Т.е. для решения задачи нам требуется найти коэффициент при (-1)–ой степени разложения функции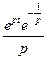 в ряд Лорана.
в ряд Лорана.
Найдем данное разложение в окрестности точки 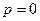 :
:
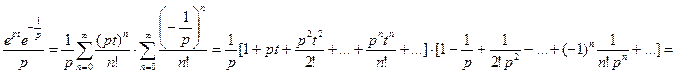
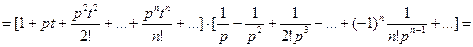
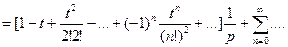 , следовательно
, следовательно
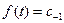
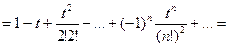
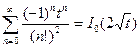
Ответ: 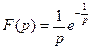
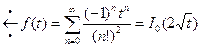 .
.
 2014-01-24
2014-01-24 992
992








