Групповая (гнездовая) выборка

Таблица 1.3

ПРЕДИСЛОВИЕ

СОДЕРЖАНИЕ

ПРЕДИСЛОВИЕ
ТЕМА 1. ТИПЫ ВЫБОРОК И ОПРЕДЕЛЕНИЕ ОБЪЕМА ВЫБОРКИ
1.1. Этапы проектирования выборки
1.2. Типы плана выборочного контроля
1.3. Стратифицированная выборка
1.4. Групповая (гнездовая) выборка
1.5. Определение объема выборки при оценке среднего
1.6. Определение объема выборки при работе с выборочными долями
ТЕМА 2. СБОР ПЕРВИЧНОЙ ИНФОРМАЦИИ
2.1.Характеристика методов проведения опросов
2.2. Сбор информации посредством анкетирования
2.3. Сбор информации посредством наблюдения
2.4. Эксперимент и имитационное моделирование
ТЕМА 3. РАЗРАБОТКА АНКЕТЫ ДЛЯ СБОРА ПЕРВИЧНОЙ ИНФОРМАЦИИ
3.1. Этапы разработки вида анкеты и корректировка вопросов
3.2. Этапы определения последовательности вопросов и завершение разработки анкеты
ТЕМА 7: ИЗМЕРЕНИЯ В МАРКЕТИНГОВЫХ ИССЛЕДОВАНИЯХ
7.1 Основы измерений
7.2. Классификация и оценка ошибок
7.3 Измерение ожиданий, восприятия и предпочтений
ТЕМА 4. АНАЛИЗ ДАННЫХ
4.1. Редактирование и кодирование данных.
4.2. Табулирование данных.
4.3. Методы анализа документов
ТЕМА 5. РЕАЛЬНЫЕ ПРОЦЕДУРЫ И СИСТЕМАТИЧЕСКИЕ ОШИБКИ СБОРА ДАННЫХ
5.1. Влияние и значение систематических ошибок
5.2. Понятие и сущность ошибок ненаблюдения
5.3. Понятие и сущность ошибок наблюдения
ТЕМА 6. ЭКСПЕРТНЫЕ ОЦЕНКИ
6.1.Общая характеристика экспертных оценок
6.2.Типы экспертных опросов
6.3.Порядок проведения экспертных опросов
СПИСОК ИСПОЛЬЗОВАННОЙ И РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

Маркетинговые исследования – сложная и комплексная процедура. Она включает в себя ряд вопросов, на которые нужно найти ответы, и набор решений, которые необходимо применять согласно методике, выбранной для достижения результата исследования. Без учета наработок, изложенных в данном курсе, студент легко может ошибиться в тонкостях исследований, т.е. запутаться во фрагментах информации, и не сможет оценить общую картину в целом. Понимание целостности процесса маркетинговых исследований необходимо будущим специалистам по маркетингу.

В результате изучения дисциплины «Маркетинговые исследования» студент должен

иметь представление:

- о месте маркетинговых исследований в комплексе маркетинга;

- о целях и задачах маркетинговых исследований;

- о формулировке проблемы;

- о выборе метода сбора данных;

- о сборе данных для решения задачи;

- об анализе и интерпретации данных.

знать:

- основные понятия маркетинга, а именно: потребность, спрос, продукт, обмен, сделка, рынок;

- составляющие комплекса маркетинга;

- методику выбора целевых рынков;

- классификацию рынков;

- методы определения потребностей и проблем;

- методы проведения маркетинговых исследований;

- классификацию маркетинговой информации;

- методы сбора исходных данных;

- методы обработки полученной информации

владеть:

- методами обработки вторичной информации;

- технологией сбора маркетинговой информации;

- технологией анализа данных;

- статистическими методами исследования.

уметь использовать:

- результаты маркетинговых исследований для обоснования и принятия управленческих решений по изучаемой проблеме.

Тема 1. Типы выборок и определение объема выборки

1.1. Этапы проектирования выборки

После того как точно определили задачу и заручились приемлемыми для ее решения схемой исследования и инструментами сбора данных, наступает следующий этап исследовательского проекта, который заключается в отборе тех элементов, которые будут подвергаться статистическому обследованию. Обследованию можно подвергнуть каждый элемент данной совокупности (популяции), произведя полную ее перепись. Полная перепись совокупности называется цензом.

Совокупность (популяция) - множество элементов, удовлетворяющих некоторым заданным условиям.

Существует и другая возможность, статистическому обследованию подвергается лишь некоторая часть совокупности, выборка.

Выборка – совокупность элементов подмножества большой группы объектов. По данным, полученным на этом подмножестве, делаются определенные выводы касательно всей группы. Возможность распространения выборочных данных на большую группу зависит от метода, с помощью которого была произведена выборка. Понятие совокупность (популяция) может относиться не только к людям, но и к фирмам, работающим в промышленности, к организациям розничной или оптовой торговли или даже к товарам, производимым на предприятии, и это понятие определяется как все множество элементов, удовлетворяющих некоторым заданным условиям.

Основа (база) выборки – перечень элементов, из которых будет производиться выборка, она может состоять из территориальных единиц, организаций, лиц и других элементов.

Выборочный метод эффективнее переписи всей совокупности по следующим причинам. Во-первых, полное обследование совокупности даже сравнительно небольшого размера требует очень больших материальных и временных затрат. Во-вторых, к моменту завершения переписи и обработки данных, полученная информация часто устаревает. В-третьих, в некоторых случаях ценз просто невозможен. Например, если необходимо проверить соответствие реального срока службы электрических ламп расчетному, необходимо держать их во включенном состоянии до момента выхода из строя. Если исследовать таким образом весь запас ламп, будут получены достоверные сведения, но торговать уже будет нечем.

В-четвертых, проведение переписей требует привлечения большого штата сотрудников, что влечет за собой возрастание вероятности появления систематических ошибок.

Существует следующая последовательность, которой можно придержи­ваться при составлении выборки.

1 этап: Задание популяции.

2 этап: Определение основы выборки.

3 этап: Определение процедуры отбора.

4 этап: Определение объема выборки.

5 этап: Отбор элементов выборки.

6 этап: Обследование отобранных элементов.

этап: Обследование отобранных элементов.

Первый этап. Прежде всего, необходимо задать совокупность или набор элементов, которые необходимо обследовать. Например, при изучении предпочтений детей исследо­вателям необходимо решить, будет ли обследуемая по­пуляция состоять только из детей, только из родите­лей, или из тех и других.

Одна компания апробировала свои электриче­ские беспроводные «гонки» только на детях. Де­тей они привели в полный восторг. Родители от­неслись к новинке иначе. Мамам не понравилось то обстоятельство, что аттракцион не приуча­ет детей к бережному отношению к машинам, а пап не устраивало то, что серьезная вещь пре­вратилась в пустую игрушку.

Возможна и обратная ситуация. Некая фирма приступила к производству нового продукта пи­тания и развернула общенациональную реклам­ную компанию, в которой основная роль была отведена не по годам развитому ребенку. Фир­ма проверяла действенность рекламных роли­ков только на матерях, которые млели от востор­га. Дети же сочли этого «акселерата», а вместе с ним и сам рекламируемый продукт, противным. Продукту пришел конец.

В начале исследования необходимо определиться с тем, из кого или из чего будет состоять соответствующая совокуп­ность: из индивидов, семей, торговых фирм, определенных организаций и так далее. При этом необходимо также определиться и с элементами, которые должны быть исключены из популяции. Должна про­изводиться как временная, так и географическая привязка элементов, на которые в ряде случаев могут на­лагаться дополнительные условия или ограничения. Например, если речь идет об индивидах, искомая попу­ляция может состоять только из лиц старше 18 лет, или только из женщин, или только из лиц с высшим образованием.

Задача определения географических границ для це­левой популяции может представлять особую пробле­му при международных маркетинговых исследованиях, поскольку при этом возрастает неоднородность рас­сматриваемой системы. Например, относительное соот­ношение городских и сельских территорий может су­щественно изменяться от страны к стране. Территори­альный аспект может оказывать серьезное влияние на состав населения и в пределах одной страны.

Чем проще определяется целевая популяция, тем выше ее охват и тем легче и дешевле процедура формирования выборки.

Охват – это выраженная в процентах доля элементов попу­ляции или группы, которые удовлетворяют условиям включения в состав выборки.

Охват прямо влияет на временные и материальные затраты, необходимые для проведения обследования. Если охват большой (то есть большая часть элементов популяции удовлет­воряет одному или нескольким простым критериям, используемым для выявления потенциальных респон­дентов), временные и материальные затраты, потреб­ные для сбора данных, сводятся к минимуму. И, наобо­рот, с увеличением количества критериев, которым должны удовлетворять потенциальные респонденты, возрастают и материальные, и временные издержки, потребные для их выявления.

Второй этап процесса отбора выборки состоит в оп­ределении основы выборки, которая является перечнем элементов, из которых будет производиться выборка. Например, пусть целевой совокупностью какого-то исследования являются все семьи, прожи­вающие в пределах Минска. Хорошей и легкодоступной основой выборки может стать телефон­ный справочник Минска. Тем не менее, при более вни­мательном рассмотрении становится очевидным, что содержащийся в справочнике список семей не вполне корректен, т.к. номера некоторых семей в нем опуще­ны (разумеется, в него не входят и семьи, не имеющие телефона), некоторые же семьи имеют по несколько телефонных номеров. Лица, недавно поменявшие мес­то жительства и соответственно номер своего телефо­на, также не присутствуют в справочнике.

Поэтому, точное соответствие между основой выборки и инте­ресующей целевой совокупностью наблюдается очень редко. Один из наиболее творческих этапов ра­боты при выборочном контроле — это определение подходящей основы выборки в тех случаях, когда со­ставление списка элементов совокупности вызывает затруднения. Подобные ситуации могут возникать при выборочном наблюдении территориальных зон или организаций с последующим взятием подвыборок, ког­да, например, целевой популяцией являются индивиды, но точного текущего их списка в наличии нет.

Третий этап процедуры составления выборки тесно связан с определением основы выборки. Выбор метода или процедуры составления выборки во многом зави­сит от принятой исследователем основы выборки. Раз­личные типы выборок требуют различных типов ос­нов выборки. Об этом будет сказано в следующих вопросах.

Четвертый этап процедуры составления выборки состоит в определении объема выборки. Этот этап будет рассмотрен в вопросе: «Определение объема выборки».

На пятом этапе необходимо реально отобрать элементы, кото­рые будут подвергнуты исследованию. Используемый для этого способ определяется избранным типом вы­борки. И, нако­нец, необходимо реально исследовать выделенных респондентов. На этом этапе существует большая вероятность совершения ряда ошибок о которых будет сказано в теме: «Реальные процедуры и систематические ошибки сбора данных»

1.2. Типы плана выборочного контроля

Все техники контроля выборки могут быть разделе­ны на две категории: наблюдение завероятностными и за детерминированными (квотными) выборка­ми.

Вероятностная выборка – это выборка, в которую каждый член совокуп­ности может включаться с некоторой заданной ненулевой вероятностью. Вероятности включения в выборку тех или иных членов совокупности могут отличаться друг от друга, но вероятность включения в нее каждого эле­мента известна. Эта вероятность определяется особой механической процедурой, используемой для отбора элементов выборки.

Детерминированная выборка – это выборка, основываемая на некоторых частных предпочтениях или суждениях, обуславливающих отбор тех или иных элементов, при этом оценка вероятности включения в выборку произвольного элемента совокупности становится невозможной. Гарантировать репрезентативность та­кой выборки нельзя. Например, за рубежом все зарегистрирован­ные избиратели с какой-то вероятностью могут быть призваны для участия в суде присяжных. Если бы все заседатели отбирались случайным образом, жюри при­сяжных представляло бы собой пример вероятностной выборки. Однако там ни для кого не секрет, что подбор присяжных заседателей — вещь, мягко говоря, не­простая. Ответчик платит своему поверенному лицу еще и за его умение подбирать потенциально «дружественное» жюри. Стало быть, жюри является образчиком детерминированной выборки.

Все детерминированные выборки основаны на частной позиции, суждении или предпочтении, а не на механической процедуре отбора элементов выбор­ки. Эти предпочтения порой могут давать хоро­шие оценки характеристик совокупности, однако не существует способа объективного определения соот­ветствия выборки поставленной задаче.

Выборки могут подразделяться также навыборки фиксированного объема и последовательные вы­борки.

Выборка фиксированного объема (фиксированная выборка) – выборка, определение объема которой производится априорно, потребная информация определяется по отобранным элементам.

При работе с выборками фиксированного объе­ма объем выборки определяется до начала обследова­ния и анализу результатов предшествует сбор всех необходимых данных. При маркетинговых исследованиях обычно используется именно выборки фиксированного объе­ма (однако не следует за­бывать, что существуют и последовательные выбор­ки, которые могут быть использованы с каждым из обсуждаемых ниже основных планов выборочного ис­следования).

Последовательная выборка – выборка, формируемая на основании серии последовательных решений. Если после рассмотрения малой выборки результат представляется неубедительным, рассматривается выборка большего объема, если и этот шаг не приводит к результату, объем выборки вновь увеличивается и так далее. Таким образом, на каждом этапе принимается решение о том, можно ли считать полученный результат достаточно убедительным или же нет.

Работа с последовательной выборкой дает возможность оце­нить тренд данных по мере их сбора, что позволяет сократить расходы, связанные с дополнительными на­блюдениями, в тех случаях, когда их целесообразность невелика.

Как вероятностный, так и детерминированный план выборочного наблюдения делятся на ряд типов (рис.1.1).

Непропорциональная

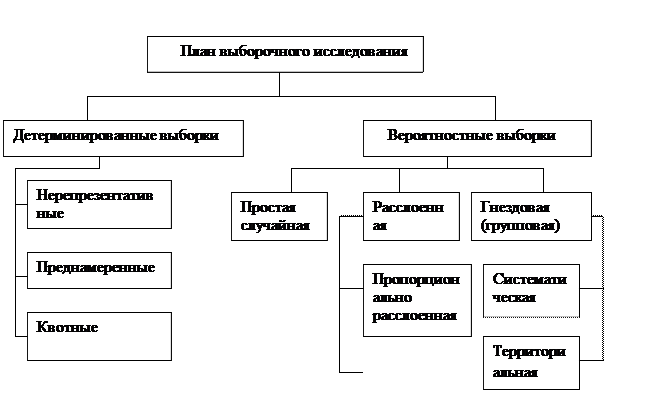
Рис. 1.1. Классификация техник выборочного контроля

Следует помнить о том, что основ­ные типы выборок могут сочетаться, образуя более сложные планы выборочного наблюдения.

При отборе элементов детерминированной выборки определяющую роль иг­рают частные оценки или решения. Иногда эти оценки исходят от исследователя, в некоторых же случаях отбор элементов совокупности определяется счетчи­ками. Т.к. элементы отбираются не механиче­ски, определение вероятности включения в выборку произвольного элемента и соответственно ошибки выборочного наблюдения становится невозможным, незнание ошибки, обусловленной избранной проце­дурой выборочного обследования, не позволяет оценить точность их оценок.

Нерепрезентативные выборки иногда называют­ся случайными, т.к. отбор элементов выборки осуществляется «случайным» образом, — отбирают­ся те элементы, которые являются или представляют­ся наиболее доступными в период проведения отбора.

Например, наша повседневная жизнь изобилует примерами по­добных нерепрезентативных выборок. Мы беседуем с приятелями и на основании их реакций и позиций дела­ем выводы касательно царящих в обществе политиче­ских пристрастий; местная радиостанция призывает лю­дей выразить свое отношение к какому-то спорному вопросу, выражаемое ими мнение интерпретируется, как превалирующее; мы призываем к сотрудничеству добровольцев и работаем с теми, кто вызывается по­мочь нам.

Проблема нерепрезентативных выборок очевид­на, — нельзя быть увереным в том, что выборки такого рода действительно представляют целевую по­пуляцию. И если мы еще можем усомниться в том, что мнение наших приятелей правильно отражает по­литические взгляды, превалирующие в обществе, нам зачастую хочется верить в то, что выборки большего объема, отобранные подобным же образом, репре­зентативны. Покажем ошибочность подобного допу­щения на примере.

Несколько лет тому назад одна из локальных теле­визионных станций города проводила ежедневный опрос общественного мнения по темам, представляющим интерес для мест­ной общины. Опросы общественного мнения, носив­шие название «Пульс Мэдисона», проводились следу­ющим образом. Каждый вечер во время шестичасовых новостей станция обращалась к зрителям с вопросом, касающимся определенной спорной проблемы, на ко­торый необходимо было дать положительный или от­рицательный ответ. В случае положительного ответа надлежало звонить по одному, в случае отрицательно­го ответа — по другому телефону. Количество голосов «за» и «против» подсчитывалось автоматически. В де­сятичасовом выпуске новостей сообщались результа­ты телефонного опроса. Каждый вечер на студию зво­нило от 500 до 1000 человек, желавших выразить свою позицию по тому или иному вопросу; телевизионный комментатор интерпретировал результаты опроса как господствующее в обществе мнение.

В одном из шестичасовых выпусков зрителям был предложен следующий вопрос: «Не считаете ли вы, что возрастной ценз на употребление алкоголя может быть снижен до 18 лет?» Существовавший легальный ценз соответствовал 21 году. Аудитория отреагирова­ла на этот вопрос необычайной активностью, — в этот вечер на студию позвонили почти четыре тысячи чело­век, из которых за снижение возрастного ценза выска­зались 78 %. Представляется очевидным, что выборка из четырех тысяч человек «должна быть репрезента­тивной» для сообщества, состоящего из 180000. Ни­чего подобного. Скорее всего определенная возрастная группа населения была за­интересована в известном исходе голосования куда сильнее прочих. Соответственно, не было ничего уди­вительного в том, что при обсуждении этого вопроса, проходившем несколькими неделями позже, выясни­лось, что во время, отведенное для опроса, студенты действовали согласованно. Они звонили на телевиде­ние по очереди, причем каждый из них совершал по несколько звонков. Таким образом, ни размер выбор­ки, ни процент поборников либерализации закона не являлись чем-то удивительным. Выборка была нере­презентативной.

Простое увеличение объема выборки не делает ее репрезентативной. Репрезентативность выборки обес­печивается не ее объемом, но надлежащей процедурой отбора элементов. Когда участники опроса определя­ются добровольно или элементы выборки отбираются в силу их доступности, план контроля выборки не дает гарантии ее представительности. Эмпирические дан­ные свидетельствуют о том, что выборки, формирова­ние которых определялось соображениями удобства, вне зависимости от их размера редко оказываются ре­презентативными.

Не рекомендуется использовать нерепрезента­тивные выборки при проведении описательных или каузальных исследований. Они допустимы лишь при поисковых исследованиях, имеющих целью отработку определенных идей или представлений, но даже и в этом случае предпочтительнее использовать предна­меренные выборки.

Преднамеренные выборки (называются не вполне случайными) – детерминированные выборки элементы которых, отвечающие целям обследования, отбира­ются вручную. Основа отбора — мнение о том, что отбираемые элементы могут дать полно­ценное представление об изучаемой популяции. Например, с ха­рактерным образчиком преднамеренной выборки мы сталкиваемся каждые четыре года во время президент­ских выборов, когда вниманию телезрителей представ­ляется углубленный анализ общественного мнения. Эти мнения считаются репрезентативными, по­скольку по опыту прошлых выборов выявляемый здесь победитель впоследствии становился президентом. Благодаря мониторингу анализа общественного мнения ана­литики могут давать долговременные прогнозы о том, кто именно победит на выборах. Хотя подобные ана­лиз и прогнозирование в последнее время претерпели существенные изменения, в их ходе по-прежнему используются преднамеренные выборки.

В некоторых случаях элементы выборки отбираются не в силу их репрезентативности, но бла­годаря тому, что они могут предоставить интересующую информацию. Например, когда суд руко­водствуется показаниями экспертизы, он, в известном смысле, прибегает к использованию преднамеренной выборки. Подобная же позиция может использоваться и при разработке исследовательских проектов.

При пер­вичной проработке вопроса интерес представлен, прежде всего, в определении перспектив исследова­ния, что и обусловливает отбор элементов выборки.

Выборка по методу «снежного кома» является одним из типов преднамеренной выборки, используе­мой при работе с особыми видами совокупностей. Эта выборка зависит от умения исследователя задать на­чальное множество респондентов, которые обладают по­требными характеристиками. Затем эти респонденты используются в качестве основы, которая определяет дальнейший отбор индивидов с нужными характерис­тиками.

Например, компания хочет оце­нить потребность в некоем изделии, которое позволило бы глухим людям общаться по телефону. Исследовате­ли могут начать разработку этой проблемы с иденти­фикации ключевых фигур обследуемой совокупности; последние могли бы назвать имена других членов этой группы, которые согласились бы принять участие в обследовании. Выборка при подобной тактике растет подобно снежному кому.

На начальных этапах проработки проблемы, когда определяются перспек­тивы и возможные ограничения планируемого иссле­дования, использование преднамеренной выборки мо­жет быть очень эффективным. Однако использование преднамеренных выборок при описательных или при каузальных исследованиях может повлиять на качество их результатов.

Квотная выборка – детерминированная выборка, отбираемая таким образом, что доля элементов выборки, обладающих определенными характеристиками, примерно соответствует доле таких же элементов в обследуемой совокупности, т.е. каждому задается квота, определяющая характеристики населения.

В качестве примера можно рассмотреть попытку создания репрезентативной вы­борки студентов, проживающих на территории уни­верситета. Если в некой выборке, состоящей из 500 индивидов, не будет ни одного старшекурсника, то вправе усомниться в ее репрезентативности и в правомерности применения полученных на этой вы­борке результатов к обследуемой совокупности. При работе с пропорциональной выборкой исследователь может проследить за тем, чтобы доля старшекурсни­ков в выборке соответствовала их доле в общем коли­честве студентов.

Предположим, что исследователь проводит выбо­рочное исследование студентов университета, при этом он заинтересован в том, чтобы выборка отражала не только их принадлежность к тому или иному полу, но и распределение их по курсам. Пусть общее число студентов составляет 10 000, из них: 3200 — первокурсни­ки, 2600 — второкурсники, 2200 — студенты третье­го курса и 2000 — выпускники; из них 7000 юношей и 3000 девушек. Для выборки объемом 1000 человек план пропорционального выборочного контроля тре­бует наличия 320 первокурсников, 260 второкурсни­ков, 220 третьекурсников и 200 выпускников, 700 юношей и 300 девушек. Исследователь может реализо­вать этот план, наделив каждого интервьюера опреде­ленной квотой, которая будет определять, с какими студентами он или она должны контактировать. Ин­тервьюеру, которому надлежит провести 20 интервью, может быть дана инструкция опросить:

• шесть первокурсников — пять юношей и одну де­вушку;

• шесть второкурсников — четырех юношей и двух девушек;

• четырех третьекурсников — трех юношей и одну девушку;

• четырех выпускников — двух юношей и двух де­вушек.

Заметьте, что отбор конкретных элементов выборки определяется не исследовательским планом, а вы­бором интервьюера, призванного соблюдать только те условия, которые были заданы квотой: опросить пяте­рых первокурсников, одну первокурсницу и так далее.

Заметьте также, что данная квота точно отобража­ет половое распределение студенческой популяции, но несколько искажает распределение студентов по кур­сам; 70% (14 из 20) интервью приходится на долю юно­шей, но лишь 30% (6 из 20) на долю первокурсников, в то время как те составляют 32% от общего числа сту­дентов. Квота, выделяемая каждому конкретному ин­тервьюеру, может не отражать и обычно не отражает распределение контрольных характеристик в популя­ции, — соответствующей пропорциональностью дол­жна обладать только итоговая выборка.

Поэтому эти вы­борки зависят скорее от личных, субъективных по­зиций или суждений, чем от объективной процедуры отбора элементов выборки. Причем, в отличие от пред­намеренной выборки, личное суждение здесь принад­лежит не разработчику проекта, а интервьюеру.

Поэтому необходимо сделать три замечания. Во-первых, выборка может сильно отличать­ся от популяции по каким-то иным важным характе­ристикам, что может оказать серьезное влияние на результат. Например, если исследование будет посвя­щено проблеме бытующих в студенческой среде предрассудков, связанных с местом проживания, небезразличным обстоятельством может оказаться то, откуда прибыли опрашиваемые — из города или из сельской местности. Поскольку квота для характеристики «выходец из города/села» не была означена, точное отображение этой характеристики становится маловероятным. По этому, исходя из этого, существует следующая альтернатива — определить квоты для всех по­тенциально значимых характеристик. Но увели­чение количества контрольных характеристик приво­дит к усложнению спецификации. Это, в свою очередь, затрудняет (а иногда и делает невозможным) отбор элементов выборки и, следовательно, приводит к удорожанию. Если, например, принадлежность к городскому или сельскому населению и социоэкономический статус также окажутся значимыми для исследования, то интервьюеру, возможно, придется заняться поисками первокурсника, который был бы горожанином и принадлежал к высшему или к средне­му классу. Иметь же дело с обычным пер­вокурсником обычно проще.

Во-вторых, убедиться в том, что данная выборка дей­ствительно является репрезентативной, очень слож­но. Можно проверить выборку на предмет соответствия распределения характеристик, которые не входят в число контрольных, их распределению в совокупности. Однако подобная проверка может приво­дить только к негативным выводам. Выявить мож­но только расхождение распределений. Если же рас­пределения выборки и совокупности для каждой из этих характеристик и повторяют друг друга, существует ве­роятность того, что выборка отличается от совокупности по какому-то иному, не заданному явно признаку.

В-третьих, интервьюеры, пре­доставленные самим себе, слишком часто прибегают к опросу своих приятелей. А так как те зачастую оказыва­ются подобными самим интервьюерам, возникает опас­ность ошибки. Например, при необходимости совершения домашних визитов интер­вьюеры зачастую оказываются движимыми соображе­ниями удобства. Например, они могут проводить опросы только днем, что приводит к недооценке мнения работающих респондентов. Помимо прочего, они не заходят в обветшавшие дома и, как правило, не поднимаются на верхние этажи зданий, не имеющих лифтов.

В зависимости от специфики изучаемой проблемы названные тенденции могут приводить к разного рода ошибкам, исправление же их на стадии анализа данных очень затруднено.

С другой стороны, при объективном отборе элементов выборки получают определенные средства, позволяющие упростить процедуру оценки репрезентативности данной выбор­ки. При анализе проблемы репрезентативности таких выборок рассматривается не столько со­став выборки, сколько процедура отбора ее элемен­тов.

Вероятностные выборки не всегда репрезентативнее детерминированных. Более репрезентативной может оказаться и детерми­нированная выборка. Преимущество вероятностных выборок состоит в том, что они позволяют оценить возможную ошибку выборочного обследования. Если же исследователь работает с детерминированной вы­боркой, он не имеет объективного метода оценки ее адекватности целям исследования.

Вероятностные выборки делятся на простую случайную, расслоенную и гнездовую.

В про­стой случайной выборке каждый элемент, включаемый в выборку, обладает одной и той же заданной вероятно­стью попадания в число исследуемых элементов, и лю­бая комбинация элементов исходной популяции может потенциально стать выборкой. Например, если мы за­хотим составить простую случайную выборку всех студентов, числящихся в определенном колледже, нам достаточно будет составить список всех студентов, присвоить каждой значащейся в нем фамилии свой но­мер и с помощью компьютера произвести случайный отбор заданного количества элементов.

Представьте, что исследуемой генеральной совокупностью является все взрослое население Гомеля. Для описания этой совокупности может быть использован ряд параметров: средний возраст, доля населения с высшим образовани­ем, уровень доходов и так далее. Обратите внимание на то, что все эти показатели имеют определенное значе­ние. Разумеется, мы можем рассчитать их, проведя пол­ную перепись изучаемой совокупности. Обычно же мы опираемся не на ценз, а на отбираемую нами выборку и используем полученные при выборочном наблюдении значения для определения искомых параметров сово­купности.

Параметр - определенная характеристика или показатель генеральной или изучаемой совокупности.

Приведем пример гипотетической совокупности, состоящей из 20 человек (табл. 1.1).

Таблица 1.1

Данные по гипотетической совокупности

Элемент	Доход	Образование лет	Подписка на газету	Элемент	Доход	Образование лет	Подписка на газету
1А 2В 3С 4D 5E 6F 7G 8H 9I 10J	5600 6000 6400 6800 7200 7600 8000 8400 8800 9200	7 8 9 9 10 11 11 11 11 11	X Y X Y X Y X Y X Y	11K 12L 13M 14N 15O 16P 17Q 18R 19S 20T	9600 10000 10400 10800 11200 11600 12000 12400 12800 13200	12 12 13 13 14 15 15 16 17 17	X Y X Y X Y X Y X Y

Работа с небольшой гипотети­ческой совокупностью имеет ряд преимуществ. Во-первых, небольшой объем выборки дает возможность легко вычислить параметры сово­купности, которые могут использоваться для ее опи­сания. Во-вторых, этот объем позволяет понять, что может произойти при принятии того или иного плана выборочного контроля. Обе эти особенности делают простым сравнение результатов выборки с «истин­ным» (известным) значением совокуп­ности, чего нельзя сказать о типичной ситуации, при которой действительное значение совокупности не­известно. Сравнение оценки с «истинным» значением приобретает в этом случае особую наглядность. Оценка параметров проводится по средней элементов, составляющих совокупность и дисперсии генеральной совокупности.

Производная совокупность – совокупность всех возможных различимых выборок, которые могут быть выделены из генеральной совокупности по заданному плану выборочного контроля. Значение статистики, используе­мое для оценки определенного параметра, зависит от выборки, определяемой планом.

Статистика – характеристика или показатель выборки.

Различные выборки дают различные статистики или оценки одного и того же параметра совокупности. Например, рассмотрим произвольную совокупность всех возможных выборок, которые могут быть выделены из гипотетической генеральной совокупности, состоящей допустим из 20 индивидов, где у каждого будут свой средний доход и имя. По плану выборочного контроля, предполагающему, что выборка объемом n=2 может быть получена путем случайного бесповторного отбора. Данные индивидов записывают на диск, после чего все диски опускают в емкость и перемешивают. Затем извлекают диск из емкости, списывают с него информацию и откладывают его в сторону. Тоже проделывают и со вторым диском. Потом возвращают оба диска в емкость, опять перемешивают и повторяют ту же последовательность действий. Для 20 дисков возможны 190 таких парных комбинаций. Для каждой комбинации вычисляют среднюю величину дохода и величину ошибки (табл.1.2).

Таблица 1.2

Данные по произвольной совокупности всех возможных выборок

Выборка	Выборка	Выборка
K	пара	средний доход	K	пара	средний доход	K	пара	средний доход
1 2 … 19 20 21 … 37 38 39 … 54 55 56 … 70 71 72 … 85 86 87 … 99 100	AВ AС … AТ BА BС … BТ C C … C D D … D E E … E F F … F G	5800 6000 … 9400 6200 6400 … 9600 6600 6800 … 9800 7000 7200 … 10000 7400 7600 … 10200 7800 8000 … 10400 8200	101 … 112 113 114 … 124 125 126 … 135 136 137 … 145 146 147 … 154 155 156 … 162 163 164	G … G H H … H I I … I J J … J K K … K L L … L M M	8400 … 10600 8600 8800 … 10800 9000 9200 … 11000 9400 9600 … 11200 9800 10000 … 11400 10200 10400 … 11600 10600 10800	… 169 170 171 … 175 176 177 … 180 181 182 183 184 185 186 187 188 189 190	… M N N … N O O … O P P P P Q Q Q R R S	… 11800 11000 11200 … 12000 11400 11600 … 12200 11800 12000 12200 12400 12200 12400 12600 12600 12800 13000

Недостатки производной совокупности. Во-первых, составление совокупностей такого рода требует слишком большой траты времени и сил. Во-вторых, совокупность определяется как совокупность всех возможных различных выборок, которые могут быть выделены из генеральной совокупности по заданному плану выборочного контроля. При изменении любой части выборочного контроля производная совокупность также меняется. Например, если возвращать в емкость первый диск прежде чем вынуть второй, производная совокупность будет включать выборки АА, ВВ, СС и так далее (а должно быть АВ, АС, ВС). Если объем бесповторных выборок будет равен 3, а не 2, появятся выборки типа АВС, и их будет не 190, а 1140. В-третьих, при изменении простого случайного отбора на любой другой метод определения элементов выборки производная совокупность также изменится.

Формирование простой случайной выборки. В выше приведенном примере отбор элементов выборки осуществлялся с помощью емкости, в которой находились все элемен­ты исходной совокупности. Это позволило нагляд­но представить понятия производной совокупности и выборочного распределения. Применять же подобный метод на практике не рекомендуется, т.к. при этом повышается вероятность ошибки. Диски могут отли­чаться и размерами, и фактурой, что в известных слу­чаях может приводить к предпочтению одних дисков другим.

Предпочтительный метод формирования простой случайной выборки основан на использовании таблицы случайных чисел. Использование такой таблицы пред­полагает следующую последовательность шагов.

Во-первых, элементам генеральной совокупности долж­ны быть присвоены последовательные номера от 1 до N. В нашей гипотетической совокупности элементу А был присвоен номер 1, элементу В — номер 2 и так далее.

Во-вторых, количество разрядов таблицы слу­чайных чисел должно быть таким же, как у номера N. Для N = 20 будут использоваться двузначные числа; для N между 100 и 999 — трехзначные числа и так далее.

В-третьих, начальная позиция должна опреде­ляться случайным образом. Можно раскрыть со­ответствующую таблицу случайных чисел и методом «тыка» формировать выборку. Посколь­ку числа в таблице случайных чисел следуют в случай­ном порядке, начальная позиция не имеет особого значения. И, наконец, можно двигаться в любом про­извольно выбранном направлении — вверх, вниз или поперек — отбирая те элементы, номера которых бу­дут соответствовать случайным числам из таблицы.

1.3. Стратифицированная выборка

Стратифицированная выборка — это вероятно­стная выборка, для которой характерна следующая двухшаговая процедура:

1) Генеральная (исходная) совокупность делится на ряд непересекающихся, исчерпывающих ее под­множеств,

2) В каждом подмножестве или группе производит­ся независимый отбор элементов простых слу­чайных выборок.

Подмножества, на которые подразделяется гене­ральная совокупность, называются слоями или част­ными совокупностями. Данное определение требует, чтобы выделяемые подмножества не пересе­кались и исчерпывали исходную совокупность. Это означает, что каждый элемент совокупности должен входить в один и только один из слоев; при этом проце­дура распределения должна охватывать все без исклю­чения элементы генеральной совокупности.

Вер­немся к рассматривавшейся в предыдущем вопросе гипо­тетической совокупности, состоящей из 20 индивидов. Эта совокупность может быть описана несколькими параметрами, таки­ми как средний уровень доходов, образовательный уровень, часть совокупности, подписавшаяся на то или иное издание. Предположим, мы хотим разделить ге­неральную совокупность на два слоя на основе обра­зовательного уровня (табл.1.1). Элементы А-J образуют первую страту или слой (уровень образо­вания соответствует не более чем 12-летнему сроку обучения), элементы К-T образуют вторую стра­ту или слой (уровень образования соответствует бо­лее чем 12-летнему сроку обучения). Число страт не обязательно должно равняться двум. Генеральная со­вокупность может быть разделена на любое другое количество страт. Мы остановились на числе 2 толь­ко потому, что оно позволяет наглядно продемонст­рировать технический аспект обсуждаемой процедуры (табл.1.3).

На втором этапе должен быть произведен отбор эле­ментов простой случайной выборки из каждой страты. Пусть объем выборок и на сей раз будет равен 2; это означает, что мы должны выбрать по одному эле­менту из каждой страты (в общем случае количество элементов из того или иного слоя не обязательно дол­жно быть одинаковым).

Распределение данных по стратам

Элементы 1 страты	Элементы 2 страты
A B C D E	F G H I J	K L M N O	P Q R S T

Процедура отбора элементов внутри стратифициро­ванной выборки ничем не отличается от аналогичной процедуры для простой случайной выборки. Элемен­там генеральной совокупности каждой страты присва­иваются порядковые номера от 1 до 10. Далее для от­бора элементов может быть использована таблица случайных чисел. Первый элемент отбирается из 10 элементов первой страты, второй — из 10 элементов второй страты; при этом возможен как повторный «вход» в таблицу случайных чисел, так и продолжение движения по избранной ранее строке или столбцу, ко­торое в любом, случае должно продолжаться до появ­ления первого числа от 1 до 10.

Рассмотрим производную совокупность.

Хотя реально может быть отобрана только одна вы­борка с объемом 2, рассмотрим производную совокупность всех возможных выборок с объемом 2, которые можно сформировать по заданному плану выборочного отбора (табл.1.4).

Таблица 1.4

Распределение данных по стратам

K	Пара	Среднее	K	пара	Среднее	K	пара	Среднее	K	пара	Среднее
	AK AL AM AN AO AP AQ AR AS AT BK BL BM BN BO BP BQ BR BS BT CK CL CM CN CO			CP CQ CR CS CT DK DL DM DN DO DP DQ DR DS DT EK EL EM EN EO EP EQ ER ES ET			FK FL FM FN FO FP FQ FR FS FT GK GL GM GN GO GP GQ GR GS GT HK HL HM HN HO			HP HQ HR HS HT IK IL IM IN IO IP IQ IR IS IT JK JL JM JN JO JP JQ JR JS JT

При заданном плане выборочного отбора возможны только 100 парных комбинаций эле­ментов, тогда как при отборе простой случайной вы­борки существовало 190 таких вариантов. Причина в том, что при таком виде выборочного наблюдения из каждой страты может быть выбран только один эле­мент. При формировании же простой случайной вы­борки из генеральной совокупности могли быть отобраны любые 2 элемента. В этом отно­шении стратифицированная выборка отличается от случайной большим числом ограничений. Каждый элемент имеет одинако­вую вероятность включения в выборку, равную 1/10, поскольку каждый из них может стать элементом, от­бираемым из той или иной страты, т.е. в пределах страты речь идет о простой случайной выборке. Равновероят­ный отбор элементов может быть присущ и другим спо­собам. Равновероятный отбор является необходимым, но не достаточным условием простого случайного вы­бора, его необходимо дополнить условием равной ве­роятности любой возможной комбинации из n элемен­тов.

Одно из преимуществ стратифицирован­ной выборки - такая выборка обеспечивает большую точность выборочных статистик, чем простая слу­чайная выборка. Например, если количественным признаком стратификации будет образование, то количество выбо­рочных средних, сильно отклоняющихся от генераль­ного среднего, существенно сократится.

Второй довод в пользу стратифицированных выбо­рок состоит в том, что разделение позволяет обследо­вать интересующие исследователя характеристики оп­ределенных подмножеств. Например, так, при стратификации можно гарантировать представление лиц с образова­нием не выше среднего и с образованием выше средне­го. Эта возможность приобретает особую значимость при отборе элементов генеральной совокупности, включающей в себя редкие сегменты. Представим, на­пример, что производитель колец с бриллиантами хочет изучить социальный состав потребителей его про­дукции. Если не будут приняты специальные меры, окажется, что высшие слои общества, составляющие всего около 3 % населения, либо вообще не будут представлены в выборке, либо окажутся представлен­ными недостаточно полно. Тем не менее, производите­ля ювелирных изделий должен интересовать именно этот немногочисленный сегмент совокупности.

В марке­тинге возможны ситуации, когда поведение совокупности, например уровень потребления какой-то продук­ции, определяется ее небольшим подмножеством. В этих случаях становится важным адекватное представление этого подмножества в обследуемой вы­борке. Стратифицированное выборочное наблюдение является одним из вариантов обеспечения названного представления.

Предпочтение стратифицированной выборки по отношению к простой случайной, определяется стоимостью и точностью, т.к. хотя стратифицированные выборки дают более точные оценки, они имеют и большую стоимость. Поэтому при выборе стратифицированной выборки необходимо сделать выбор между пропорционально и непропорционально стратифицированными выборками.

Пропорционально стратифицированная выборка – стратифицированная выборка, в которой межслойное соотношение наблюдений пропорционально относительной доле элементов в каждом слое генеральной совокупности.

Непропорционально стратифицированная выборка – стратифицированная выборка, в которой объем отдельных слоев или подмножеств зависит от объема и изменчивости соответствующих слоев генеральной совокупности, т.е. слои с большей изменчивостью количественного признака получают в выборке большее представление, а слои, близкие к гомогенности, меньшее представление, чем в пропорционально стратифицированной выборке.

Преимущество пропорционального распределения состоит в том, что здесь достаточно знать только относительные размеры каждой страты для определения количества выборочных наблюдений, которые должны быть отобраны из каждого слоя для заданного объема выборки. Однако непропорционально стратифицированная выборка может давать более точные результаты. При ее составлении одновременно учитывают два критерия: объем страты и ее изменчивость.

Очень часто путают стратифицированные выборки с квотными. У тех и других есть ряд сходств. В обоих случаях генеральная совокупность делится на сегменты, и элементы отбираются из каждого сегмента. Но между ними существует существенное различие. В стратифицированных выборках элементы выборки выбираются вероятностными методами; что касается квотных выборок, то их отбор обусловлен позицией исследователя.

Групповые выборки (кластерные) – еще один способ вероятностного выборочного исследования. Она в чем-то похожа, а в чем-то отличается от стратифицированного выборочного отбора.

Групповая выборка – вероятностная выборка, для которой характерна следующая двухступенчатая процедура:

1) генеральная совокупность делится на ряд непересекающихся исчерпывающих ее подмножеств;

2) производится случайный отбор подмножеств.

Если для выборки используют все элементы выбранных подмножеств, процедура называется одноступенчатой; если же выборка отбирается из этих подмножеств при помощи вероятностного метода, процедура называется двухступенчатой.

Существуют сходства и различия групповой и стратифицированной выборки. В каждом случае генеральная совокупность делится на ряд непересекающихся, исчерпывающих ее подмножеств, однако, в стратифицированной выборке производится отбор элементов из каждого подмножества, а при групповой выборке производится отбор подмножеств.

Рассмотрим пример из вопроса 2 (данные табл.1.1). Если все подписчики издания X будут рассматриваться в качестве первого, а все подписчики издания Y в качестве второго подмножества, можно достаточно уверено использовать в качестве контрольной выборки для оценки среднего уровня доходов ту или иную группу. Хотя распределение уровня доходов внутри каждого подмножества может отличаться от аналогичного распределения в генеральной совокупности, разброс значений уровня доходов таков, что при оценке среднего уровня доходов и дисперсии этого уровня по элементам любой из двух названных выборок можно допустить лишь незначительную ошибку.

Систематическая выборка – один из видов группового выборочного отбора, обеспечивающий возможность простейшего исследования многих генеральных совокупностей. Такая выборка предполагает включение в нее каждого k-го элемента генеральной совокупности, начиная с некоторого выбранного произвольно элемента. Рассмотрим старую совокупность из 20 индивидов и представим, что необходимо отобрать из них 5 элементов. Для 20 элементов совокупности и объема выборки, равного5, выборочная доля равна f=n/N=5/20=1/4, т.е. должен отбираться один элемент из четырех. Выборочный интервал I=1/f будет равен 4. это означает, что после произвольно выбранной начальной позиции должен отбираться каждый четвертый элемент. Если начальная позиция придется на 1, то в выборку будут отобраны 1-й, 5-й, 9-й, 13-й, 17-й элементы. Если позиция придется на 2, будут отобраны, соответственно, 2-й, 6-й, 10-й, 14-й, 18-й элементы и т.д.

Систематическая выборка относится к категории групповых одноступенчатых, т.к. используются все элементы выделенных групп, а не некоторая, возникающая в результате отбора их часть.

Подмножества или группы в нашем случае это:

Группа 1: A, E, I, M, Q.

Группа 2: B, F, J, N, R.

Группа 3: C, G, K, O, S.

Группа 4: D, H, L, P, T.

Для исследования производится случайный выбор одной из этих групп. В данном случае выбор делается один раз.

Достоинства систематической выборки:

- простота формирования;

- отсутствует проблема дублирования элементов в отличие от случайной выборки;

- имеет большую репрезентативность, чем простая случайная выборка.

При использовании систематической выборки существует следующая опасность, если в списке элементов наблюдается естественная периодичность, оценка, производимая на основе такой выборки, связана с серьезными ошибками. Например, известен уровень продаж авиабилетов на каждый день года, и нужно проанализировать продажи с точки зрения продолжительности полета. Анализ всех 365 дней года будет весьма дорогостоящим. Предположим, что исследовательского бюджета хватит на исследование 52 дней. Систематическая выборка с выборочным интервалом равным 7 дней (365/52) скорее всего, приведет к ошибочным выводам, т.к. будет отражать уровень продаж авиабилетов на рейсы, совершаемые по понедельникам, средам или, например, по воскресеньям.

Поэтому, правильное задание выборочного интервала возможно только на основе исследования причин периодичности.

Территориальная выборка – вид группового выборочного отбора, при котором территории или зоны (например, переписные районы, участки) выступают в роли первичных выборочных единиц. Генеральная совокупность делится (обычно с использованием карты) на ряд непересекающихся, исчерпывающих ее подмножеств или территорий, после чего формируется случайная выборка этих территорий. Если в исследовании участвуют все семьи, живущие на выделенных территориях, то имеем дело с одноступенчатой территориальной выборкой; если же исследуются не все, но лишь отобранные из первичной выборки семьи, обследование называется двухступенчатым.

Принцип, который лежит в основе систематической выборки, задействован и в территориальном выборочном отборе.

Составить точные исчерпывающие списки населения практически невозможно. Либо они просто отсутствуют, либо если и существуют, то содержат массу устаревшей недостоверной информации (люди переезжают, рождаются, умирают, женятся и разводятся). Несмотря на отсутствие списка семей, можно использовать в качестве относительно точных первичных выборочных единиц отдельные городские районы, представленные на карте.

Одноступенчатая территориальная выборка проводится на основе следующих этапов:

1) Произвести простой случайный отбор n городских кварталов из совокупности N кварталов.

2) Определить потребление товара и доходы всех семей, живущих в выделенных кварталах, и распространить выборочный показатель на всю совокупность.

Отличительной особенностью одноступенчатой территориальной выборки является регистрация и исследование всех семей, проживающих в выделенных территориальных единицах. Часто вместо сплошного исследования всех элементов выделенной группы проводится только выборочное обследование. Различают два типа двухступенчатой территориальной выборки.

1) Простая двухступенчатая территориальная выборка.

2) Территориальная выборка с вероятностями, пропорциональными объему (территориальная квотная выборка).

Простая двухступенчатая территориальная выборка – вид группового выборочного отбора, при котором из каждой первичной выборочной единицы (например, районов) отбирается определенная доля элементов выборки второго уровня (например, семей).

Рассмотрим совокупность, состоящую из 100 кварталов предположим, что в каждом квартале живут по 20 семей. Допустим, необходимо исследовать 80 семей из 2000. Таким образом, выборочная доля равна:

.

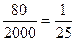Существует ряд способов формирования выборки:

1). Отбор 10 кварталов и 8 семей в каждом квартале;

2). Отбор 8 кварталов и 10 семей в каждом квартале;

3). Отбор 20 кварталов и 4 семей в каждом квартале;

4). Отбор 4 кварталов и 20 семей в каждом квартале.

Последний вариант представляет собой одноступенчатую территориальную выборку, а первые три относятся к категории двухступенчатых. Варианты, с которой будут отобраны кварталы, называются первоуровневой выборочной долей (формула 1.1):

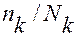, (1.1)

где n_k и N_k – количество кварталов в выборке и в генеральной

совокупности соответственно.

Для первых трех случаев первоуровневые выборочные доли равны, соответственно 1/10, 1/12,5 и 1/5.

Вероятность отбора семьи называется выборочной долей второго уровня. Т.к. выборка должна состоять из 80 семей, выборочная доля второго уровня отличается для каждого из приведенных выше вариантов (формула 1.2):

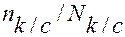_, (1.2)

где n_k/c и N_k/c – количество семей на квартал в выборке и в

генеральной совокупности.

Для первых трех схем отбора выборочная доля равна соответственно: 8/20=2/5, 10/20=1/2, 4/20=1/5. При этом произведение выборочных долей первого и второго уровней в любом случае равно общей выборочной доле 1/25. Из соображения экономии при сборе данных выборочная доля второго уровня должна быть высокой (вторая схема), но из соображений статистической эффективности выборочная доля второго уровня должна быть небольшой. Поэтому статистические соображения свидетельствуют в пользу третьей схемы. Простая двухступенчатая территориальная выборка эффективна, если количество единиц второго уровня (семья) на единицу первого уровня (квартал) сохраняется примерно равным. Если количество единиц второго уровня существенно отличаются друг от друга, простая двухступенчатая выборка может привести к ошибочным оценкам. Например, в некоторых кварталах могут находиться многоэтажные дома, где проживают семьи с низким доходом. В богатых кварталах могут находиться всего несколько домов, в каждом из которых будет проживать по одной семье. Т. е., количество единиц второго уровня на единицу первого уровня окажется совершенно различным. Проблема эта снимается путем комбинирования различных территорий, или прибегают к территориальной квотной выборке.

Территориальная квотная выборка – вид группового отбора, при котором из каждой первичной выборочной единицы отбирается фиксированное количество элементов второго уровня. Вероятности, относящиеся к отбору каждой первичной единицы, могут изменяться, т.к. они напрямую связаны с относительными размерами первичных единиц.

Приведем пример на основании предыдущего. Данные приведены в табл. 1.5.

Таблица 1.5

Данные по территориальной квотной выборке

Квартал	Количество семей	Суммарное количество семей
1 2 3 4 5 6 7 8 9 10	800 400 200 200 100 100 100 50 25 25	800 1200 1400 1600 1700 1800 1900 1950 1975 2000

Пусть после анализа экономических и статистических критериев количество единиц второго уровня на единицу первого уровня было принято равным 10.для получения выборки нужного объема (20 единицам) необходимо выбрать две единицы первого уровня. Вероятность выбора определенного элемента зависит от объема единицы первого уровня. В данном случае можно прибегнуть к таблицам трехзначных случайных чисел. Для этого можно воспользоваться двумя первыми числами от 1 до 2000. Числа от 1 до 800 относятся к первому кварталу; числа от 801 до 1200 – ко второму кварталу; числа от 1201 до 1400 – к третьему и т.д.

Вероятность того, что в выборку будет включена любая конкретная семья, остается постоянной, т.к. отличия вероятностей отбора элементов первого уровня компенсируются отличиями вероятностей отбора элементов второго уровня. Допустим, к примеру, рассмотрим два полюса – 1-й и 10-й кварталы. Вероятность выделения квартала 1 равна 800/2000=2/5, т.к. 800 из возможных 2000 значений случайных чисел приходится именно на этот квартал. Кварталу 10 соответствует только 25 значений случайных чисел (от 1976 до 2000), соответственно выборочная доля первого уровня для 10 квартала равна 25/2000=1/80. Т. к. из каждого квартала следует выбрать по 10 семей, выборочная доля второго уровня для первого квартала равна 10/800=1/80, для 10 квартала 10/25=1/2,5. При перемножении соответствующих вероятностей первого и второго уровней происходит их компенсация

.

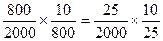Подобное соотношение верно и для других кварталов.

Достоинства территориальной квотной выборки:

- возможность избежать ошибок, присущих простой двухступенчатой территориальной выборке;

- повышение точности оценок при увеличении изменчивости количества единиц второго уровня на единицу первого уровня.