Закон Гука для сдвига. Модуль сдвига

Лекция 24 Упругие уравнения

Пример 2. Найти область сходимости функционального ряда.

Решение. Общий член ряда. Тогда последующий член ряда получается

заменой на: Вычислим предел

.

По признаку Даламбера ряд сходится, если т. е. должно выполняться неравенство Преобразуя последнее неравенс-

тво к виду получаем, что в области

ряд сходится абсолютно. Исследуем сходимость ряда на концах интервала.
При ряд имеет вид. Это сходящийся ряд обобщенный гармонический ряд ().
При ряд имеет вид. Это знакочередующийся ряд, который сходится абсолютно, так как ряд, составленный из модулей сходится. Таким образом, область сходимости исходного функционального ряда будет такой: Заметим, что нашу задачу можно было бы решить, сделав в исходном ряде замену Тогда получим так называемый степенной ряд который будет сходиться в области На следующей лекции будет показано, что этот ряд будет сходиться равномерно на любом отрезке

[1] Впредь ковычки будем опускать.

Нам уже известен закон Гука в виде:

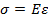
Он устанавливает связь между нормальным напряжением 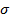при растяжении (сжатии) в каком-либо направлении и соответствующим относительным удлинением (укорочением) 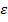. Аналогично можно сделать допущение о связи, существующей между касательным напряжением 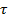при чистом сдвиге и соответствующим углом сдвига 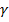. Эта связь также считается линейной.

Закон Гука для касательных напряжений напишем в виде:

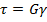
И будем применять его для любой прямоугольной частицы, на гранях которой попарно действуют касательные напряжения 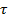, вызывающие сдвиг 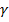. коэффициент пропорциональности G называется модулем сдвига и является величиной такого же рода, как и модуль Юнга Е, и измеряется также в МПа.

Таким образом, мы предполагаем, что относительное удлинение зависит от нормального напряжения, а сдвиг от касательного напряжения. Поэтому для характеристики идеально упругого тела необходимы три константы: модуль упругости Е, коэффициент Пуассона (поперечной деформации) 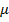и модуль сдвига G.

Эти величины связаны между собой. Рассмотрим случай, когда частица с квадратным поперечным сечением растягивается в одном направлении напряжением 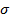, а в другом, перпендикулярным к первому сжимается напряжением 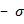, и принимает форму прямоугольника (рис.1).

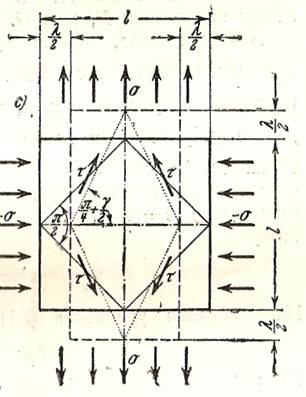
Рис.1

Наибольшие касательные напряжения лежат в плоскостях, образующих углы 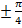с нормальными напряжениям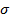и и 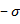. Из известного соотношения:

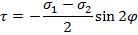
Следует, что

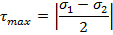
Т.е. 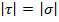, и нормальные напряжения в указанных плоскостях отсутствуют. Следовательно, при помощи этих плоскостей во взятом квадрате можно выделить квадрат, который будет находиться в условиях чистого сдвига (рис.2). Этот квадрат под действием касательных напряжений примет форму ромба (рис.1).

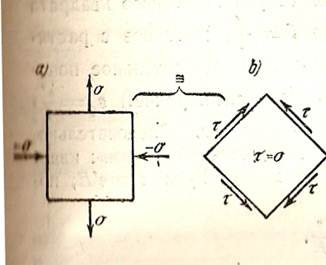
Рис.2

Очевидно, что деформация такого квадрата под действием касательных напряжений и деформация основного квадрата под действием нормальных напряжений совпадают между собой. Исходя из этого, можно найти связь между величинами Е, 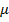G.

Вертикальная сторона основного квадрата получает относительное удлинение 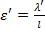, связанное с растягивающим напряжением 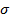, и относительное поперечное расширение 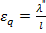, связанное со сжимающим напряжением 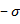. следовательно, полное относительное удлинение вертикальной стороны квадрата равно 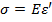, поэтому:

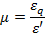
Откуда

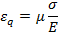
Полное относительное удлинение составит:

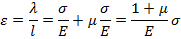
Найдем теперь угол сдвига 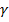вписанного квадрата, подвергающегося чистому сдвигу. Из рисунка 1 имеем соотношение:

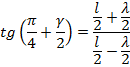
Так как угол 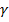очень мал, то это выражение можно переписать в виде:

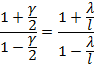
Откуда получим:

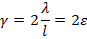
Так как на основании закона Гука для сдвига 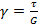и 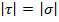, получим:

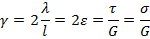
Или

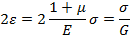
Откуда получим:

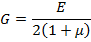
Поведение идеально упругого тела определяется только двумя из трех констант Е, 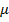или G.