.
Теорема. Если функции определены и непрерывны на отрезке и ряд сходится равномерно на к сумме, то его можно почленно интегрировать на этом отрезке
Теорема. Если члены ряда удовлетворяют неравенствам, где, а числа, не зависящие от, и, если ряд сходится, то ряд сходится равномерно на множестве X.
Теорема. Для того чтобы ряд сходился равномерно на множестве X, необходимо и достаточно, чтобы.
Функциональные ряды
Плотность распределения вероятностей непрерывной случайной величины
Рассмотрим интервал и определим вероятность того, что непрерывная случайная величина примет значения, заключённые в этом интервале. Согласно свойству 2 имеем. Разделим эту величину на ширину интервала, получим величину вероятности, приходящейся на единицу длины интервала:, которую назовём средней плотностью распределения вероятности на интервале. Введём понятие плотности распределения вероятности в данной точке, определив её как предел средней плотности на интервале при условии, что и указанный предел существует. Обозначим эту плотность распределения вероятностей через, тогда
Зная плотность распределения, можно найти функцию распределения. А именно. Таким образом:
Заметим, что закон распределения непрерывной случайной величины может быть задан как функцией распределения, так и плотностью распределения. Для дискретной случайной величины имеет смысл только функция распределения вероятностей (почему?).
Найдём вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу.. Так как
В каждой точке определения функций если принять, то функциональный ряд:
преобразуется в числовой ряд:
, который может оказаться как сходящимся, так и расходящимся.
Совокупность значений при которых функциональный ряд сходится, называется областью сходимости этого ряда.
Суммой ряда называется функция, определенная в каждой точке области сходимости ряда.
По определению предела означает, что.
Последовательность функций сходится равномерно к на множестве, если.
Ряд сходится равномерно на множестве X к сумме, если последовательность его частичных сумм сходится равномерно на множестве к функции.
v Признак равномерной сходимости, основанный на сравнении функционального ряда со сходящимся числовым.
v Достаточные условия непрерывности суммы ряда.
Теорема. Если функции определены и непрерывны на множестве X и ряд сходится равномерно к сумме S(x), то эта сумма будет непрерывна на множестве X.
v Свойства равномерно сходящихся рядов.
Теорема. Если функции определены на отрезке и существуют непрерывные производные на интервале, а ряд сходится на и равномерно сходится ряд, то сумма ряда имеет на непрерывную производную, причем,. Таким образом, ряд можно почленно дифференцировать.
.
ПРИМЕР №1. Найти сумму ряда.
ПРИМЕР №2. Найти сумму ряда.
ПРИМЕР №3. Найти область сходимости ряда.
Ряд будет сходится при Причем при - условно имеем.
Следовательно
сходится условно.
Область сходимости.
|
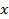 с помощью единичного отрезка
с помощью единичного отрезка 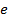 (рисунок).
(рисунок).
 | |||
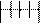 | |||
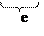 |
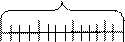
При измерении оказалось, что отрезок 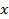 состоит из трех отрезков, равных
состоит из трех отрезков, равных 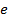 , и отрезка, который короче отрезка
, и отрезка, который короче отрезка 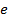 . В этом случае длина отрезка
. В этом случае длина отрезка 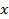 не может быть выражена натуральным числом. Однако, если отрезок
не может быть выражена натуральным числом. Однако, если отрезок 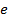 разбить на 4 равные части, то отрезок
разбить на 4 равные части, то отрезок 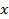 окажется состоящим из 14 отрезков, равных четвертой части отрезка
окажется состоящим из 14 отрезков, равных четвертой части отрезка 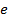 . И тогда, говоря о длине отрезка
. И тогда, говоря о длине отрезка 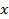 , мы должны указывать два числа 4 и 14: четвертая часть отрезка
, мы должны указывать два числа 4 и 14: четвертая часть отрезка 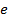 укладывается в отрезке точно 14 раз. Поэтому длину отрезка обозначают:
укладывается в отрезке точно 14 раз. Поэтому длину отрезка обозначают: 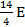 , где
, где 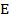 - длина единичного отрезка
- длина единичного отрезка 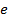 , а символ
, а символ 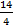 называют дробью.
называют дробью.
Определение 1. Пусть даны отрезок 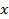 и единичный отрезок
и единичный отрезок 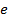 , длина которого равна
, длина которого равна 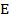 . Если отрезок
. Если отрезок 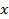 состоит из
состоит из 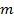 отрезков, равных -ой части отрезка
отрезков, равных -ой части отрезка 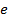 , то длина отрезка
, то длина отрезка 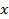 может быть представлена в виде
может быть представлена в виде 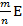 , где символ
, где символ  называют дробью (и читают «эм энных»).
называют дробью (и читают «эм энных»).
В записи  числа
числа 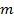 и
и 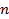 – натуральные,
– натуральные, 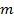 называется делителем,
называется делителем, 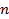 - знаменателем дроби.
- знаменателем дроби.
Дробь  называется правильной, если ее числитель меньше знаменателя дроби, и неправильной, если ее числитель больше знаменателя или равен ему.
называется правильной, если ее числитель меньше знаменателя дроби, и неправильной, если ее числитель больше знаменателя или равен ему.
Вернемся к рисунку. Очевидно это не единственный вариант выбора такой части отрезка 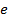 , которая укладывается в отрезке
, которая укладывается в отрезке 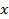 целое число раз. Можно взять восьмую часть отрезка
целое число раз. Можно взять восьмую часть отрезка 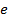 , тогда отрезок
, тогда отрезок 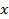 будет состоять из 28 таких частей и его длина будет выражаться дробью
будет состоять из 28 таких частей и его длина будет выражаться дробью 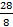 .
.
Длина одного и того же отрезка 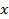 при заданном единичном отрезке
при заданном единичном отрезке 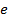 может выражаться различными дробями, причем, если длина выражена дробью
может выражаться различными дробями, причем, если длина выражена дробью  , то она может быть выражена и любой дробью вида
, то она может быть выражена и любой дробью вида 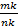 , где
, где 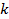 - натуральное число.
- натуральное число.
Теорема 1. Для того, чтобы дроби  и
и  выражали длину одного и того же отрезка, необходимо и достаточно, чтобы выполнялось равенство
выражали длину одного и того же отрезка, необходимо и достаточно, чтобы выполнялось равенство 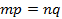 .
.
Определение 2. Две дроби  и
и  называются равными, если
называются равными, если 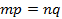 .
.
Если дроби равны, то пишут 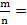
 .
.
Например, 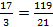 , так как
, так как 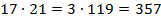 , а
, а 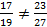 , потому что
, потому что 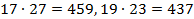 и
и 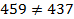 .
.
Из сформулированных выше теоремы и определения следует, что две дроби равны тогда и только тогда, когда они выражают длину одного и того же отрезка.
Теорема 2. Равенство дробей является отношением эквивалентности.
Доказательство. 1) Рефлексивность: 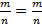 , так как
, так как 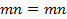 ;
;
2) Симметричность: если 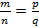 , то
, то 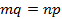 . Тогда
. Тогда 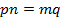 , следовательно,
, следовательно, 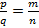 .
.
3) Транзитивность: если 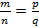 и
и 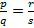 , то
, то 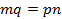 и
и 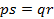 . Тогда
. Тогда 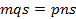 и
и 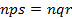 . Следовательно,
. Следовательно, 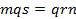 или
или 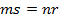 . Откуда
. Откуда 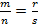 .
.
Теорема доказана.
Из определения дробей вытекает основное свойство дробей: Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной.
На этом свойстве основано сокращение дробей и приведение дробей к общему знаменателю.
Сокращение дробей – это замена одной дроби другой, равной данной, но с меньшим числителем и знаменателем.
Если числитель и знаменатель дроби одновременно делятся только на единицу, то дробь называется несократимой.
Приведение дробей к общему знаменателю – это замена данных дробей равными дробями, имеющими одинаковые знаменатели. Общим знаменателем двух дробей  и
и  является общее кратное чисел
является общее кратное чисел 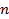 и
и 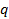 , а наименьшим общим знаменателем – их наименьшее общее кратное.
, а наименьшим общим знаменателем – их наименьшее общее кратное.
 2014-01-25
2014-01-25 764
764








