Степенным рядом называется ряд вида:
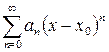 , ,
| (1) |
где 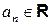 ‑ числовые коэффициенты,
‑ числовые коэффициенты, 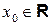 ‑ фиксированное число и
‑ фиксированное число и 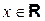 ‑ переменная.
‑ переменная.
Если зафиксировать 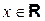 , то получится числовой ряд. Если этот числовой ряд сходится, то говорят, что степенной ряд (1) сходится в точке
, то получится числовой ряд. Если этот числовой ряд сходится, то говорят, что степенной ряд (1) сходится в точке 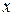 . Множество всех точек
. Множество всех точек 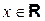 , в которых ряд (1) сходится, называют множеством сходимости ряда (1).
, в которых ряд (1) сходится, называют множеством сходимости ряда (1).
Пример. Ряд 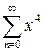 сходится абсолютно при
сходится абсолютно при 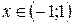 , т.к.
, т.к. 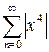 при
при 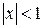 сходится. Если же
сходится. Если же 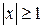 , то
, то 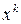 не стремится к нулю, т.е. не выполнено необходимое условие сходимости и ряд расходится. Таким образом, множеством сходимости ряда
не стремится к нулю, т.е. не выполнено необходимое условие сходимости и ряд расходится. Таким образом, множеством сходимости ряда 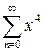 является
является 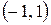 .
.
Множество сходимости всякого ряда (1) есть промежуток, середина которого находится в точке 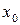 . Промежуток сходимости может быть отрезком, полуинтервалом, интервалом, бесконечным промежутком или промежутком нулевой длины, т.е. точкой
. Промежуток сходимости может быть отрезком, полуинтервалом, интервалом, бесконечным промежутком или промежутком нулевой длины, т.е. точкой 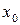 . Число
. Число 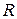 , равное половине длины промежутка сходимости, называют радиусом сходимости. Радиус сходимости ряда (1) может быть вычислен следующим образом:
, равное половине длины промежутка сходимости, называют радиусом сходимости. Радиус сходимости ряда (1) может быть вычислен следующим образом:
1. 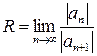 , если такой предел существует;
, если такой предел существует;
2. 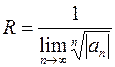 , если такой предел существует.
, если такой предел существует.
Если в формулах 2. и 3. пределы равны 0, то 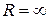 . Если пределы равны
. Если пределы равны 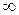 , то
, то 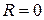 .
.
Если 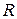 ‑ конечное число, то промежуток
‑ конечное число, то промежуток 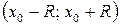 принадлежит множеству сходимости. В ряде случаев множеству сходимости могут принадлежать также точки
принадлежит множеству сходимости. В ряде случаев множеству сходимости могут принадлежать также точки 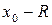 и
и 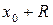 .
.
Пример. Ряд 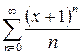 имеет радиус сходимости
имеет радиус сходимости 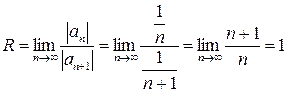 .
.
Значит, интервал 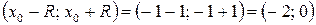 входит в промежуток сходимости. Исследуем сходимость ряда на концах интервала
входит в промежуток сходимости. Исследуем сходимость ряда на концах интервала 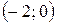 . При
. При 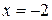 получаем ряд
получаем ряд 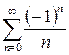 , который сходится по признаку Лейбница. При
, который сходится по признаку Лейбница. При 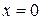 получаем ряд
получаем ряд 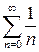 , который расходится. Таким образом, промежуток сходимости ряда – полуинтервал
, который расходится. Таким образом, промежуток сходимости ряда – полуинтервал 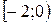 .
.
Пример. Ряд 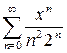 имеет радиус сходимости
имеет радиус сходимости 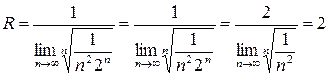 . Значит, интервал сходимости
. Значит, интервал сходимости 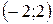 .
.
Изучим сходимость ряда на концах этого интервала. При 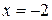 получаем ряд
получаем ряд 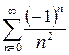 , который сходится абсолютно. При
, который сходится абсолютно. При 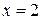 получаем ряд
получаем ряд 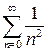 , который также сходится. Значит, промежуток сходимости – отрезок
, который также сходится. Значит, промежуток сходимости – отрезок 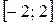 .
.
Если функция 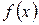 в точке
в точке 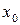 имеет производные любого порядка, то для нее можно построить степенной ряд:
имеет производные любого порядка, то для нее можно построить степенной ряд:
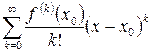
| (2) |
Этот ряд называется рядом Тейлора для функции 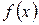 в точке
в точке 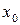 .
.
Множество сходимости ряда (2) не всегда совпадает с областью определения функции 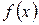 , а его сумма не обязательно равна
, а его сумма не обязательно равна 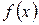 . Если сумма ряда (2) совпадает с
. Если сумма ряда (2) совпадает с 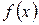 на множестве
на множестве 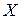 , то можно написать:
, то можно написать:
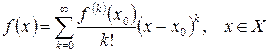
| (3) |
В этом случае говорят, что 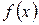 на множестве
на множестве 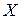 разложена в степенной ряд (3). Справедливы следующие разложения:
разложена в степенной ряд (3). Справедливы следующие разложения:
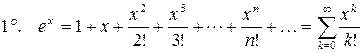 ,
, 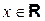 .
.
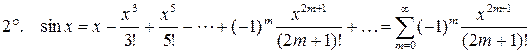 ,
, 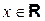
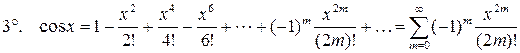 ,
, 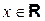 .
.
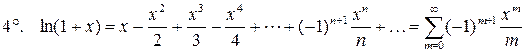 ,
, 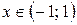 .
.
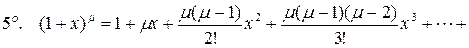
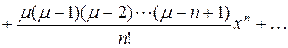 ,
, 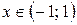 .
.
Пример. Разложить по степеням 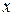 функцию
функцию 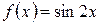 .
.
Если обозначить 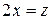 , то, используя разложение
, то, используя разложение  , получаем:
, получаем: 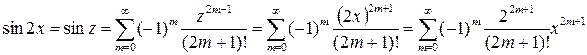 .
.
Пример. Разложить по степеням 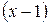 функцию
функцию 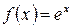 .
.
Обозначим 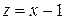 и используем разложение
и используем разложение  , получим
, получим 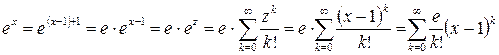 .
.
 2014-01-25
2014-01-25 706
706







