Пользуясь имеющейся операцией сложения на множестве целых чисел, введём соответствующую операцию на построенном множестве рациональных чисел: 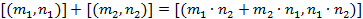 .
.
Предложение 1. Введенная операция сложения корректна, то есть не зависит от выбора представителей соответствующих классов эквивалентности.
Доказательство. Пусть 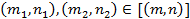 и
и 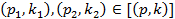 . Тогда
. Тогда 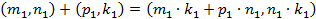 и
и 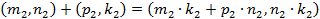 . Так как
. Так как 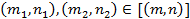 , то
, то 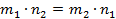 . Аналогично,
. Аналогично, 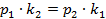 . Тогда
. Тогда 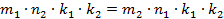 и
и 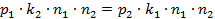 . Отсюда получаем, что
. Отсюда получаем, что 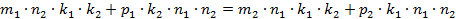 и
и 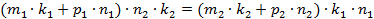 . Следовательно,
. Следовательно, 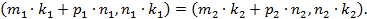
Свойства сложения:
1) Коммутативность: 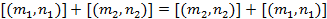
Доказательство: 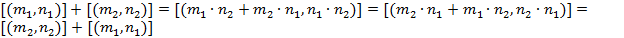 .
.
2) Ассоциативность: 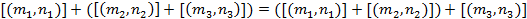 .
.
Доказательство: 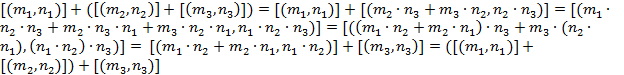 .
.
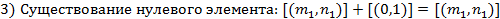 .
.
Доказательство: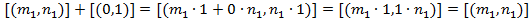
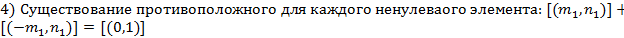 .
.
 2014-01-25
2014-01-25 730
730








