Определение 14. Осью называется прямая с фиксированным на ней единичным вектором. Этот вектор называется ортом оси.
Пусть 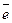 - орт оси, - орт оси, 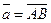 -произвольный вектор, -произвольный вектор, 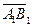 = = 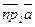 . Так как векторы . Так как векторы 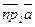 и и 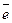 коллинеарны и коллинеарны и 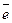 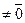 , то , то 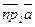 = a × = a ×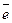 . Число a называется числовой проекцией вектора . Число a называется числовой проекцией вектора  на данную ось и обозначается прl на данную ось и обозначается прl .
Из 70 и 80 свойств векторных проекций следует .
Из 70 и 80 свойств векторных проекций следует 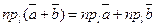 и и 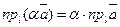 . .
| 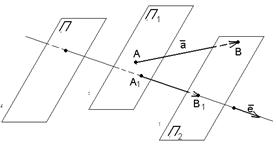 Рис. 12
Рис. 12
|
90. Векторные и числовые проекции вектора на сонаправленные оси параллельно одной и той же плоскости равны.
Доказательство. Сонаправленные оси имеют один и тот же орт. Если 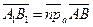 и и 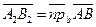 , то , то 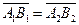 (по свойству отрезков параллельных прямых, заключённых между параллельными плоскостями). Итак, векторные (по свойству отрезков параллельных прямых, заключённых между параллельными плоскостями). Итак, векторные
| 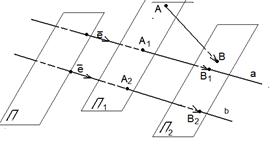 Рис. 13
Рис. 13
|
Проекции вектора на сонаправленные оси равны. Так как у этих осей один и тот же орт, то числовые проекции тоже равны.
100. Так как направление оси можно задавать любым ненулевым вектором, сонаправленным с ортом оси, то можно говорить о проекции одного вектора на направление другого и обозначать 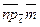 (проекция вектора
(проекция вектора 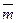 на направление вектора
на направление вектора 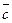 параллельно плоскости П).
параллельно плоскости П).
 2014-01-25
2014-01-25 883
883








