Пусть l – прямая, П – плоскость и l  П. Пусть М – произвольная точка. Через точку М
П. Пусть М – произвольная точка. Через точку М
| проведём плоскость П1, параллельную П. Пусть М1 = l Ç П1. Точка М1 называется проекцией точки М на прямую l параллельно плоскости П. Свойства проекций. 10. Каждая точка имеет проекцию и только одну. 20. Точка совпадает со своей проекцией тогда и только тогда, | 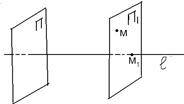 Рис. 9
Рис. 9
|
когда она лежит на прямой l.
30. Точки имеют одну и ту же проекцию тогда и только тогда, когда они лежат в одной плоскости, параллельной П.
40. Если отрезок параллелен плоскости П, то он проектируется в точку. Если отрезок не параллелен плоскости П, то его проекция – отрезок.
50. Проекция ориентированного отрезка есть ориентированный отрезок. Следовательно, проекцией вектора будет вектор. Он называется векторной проекцией данного вектора и обозначается 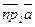 (параллельно П). Если проектирование идёт параллельно только одной плоскости, то слова в скобках можно опускать.
(параллельно П). Если проектирование идёт параллельно только одной плоскости, то слова в скобках можно опускать.
60. Равные и параллельные отрезки имеют равные проекции.
| Доказательство. Пусть отрезки [АВ] и [СD] равны и параллельны. Если [АВ] параллелен плоскости П, то [СD] тоже параллелен плоскости П. В этом случае оба отрезка проектируются в точку. Следовательно, их проекции равны. | 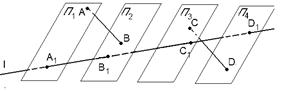 Рис. 10
Рис. 10
|
Пусть [АВ], а поэтому и [СD], не параллельны плоскости П. Пусть [АВ] проектируется в [А1В1], а [СD] - в [С1D1]. При параллельном переносе на вектор 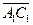 Плоскость П1 перейдёт в П3, П2 - в П4, прямая l - сама в себя. Следовательно, все отрезки с концами в плоскостях П1 и П2 перейдут в некоторые отрезки с концами в плоскостях П3 и П4. Отсюда и следует, что [А1В1] равен и параллелен [С1D1].
Плоскость П1 перейдёт в П3, П2 - в П4, прямая l - сама в себя. Следовательно, все отрезки с концами в плоскостях П1 и П2 перейдут в некоторые отрезки с концами в плоскостях П3 и П4. Отсюда и следует, что [А1В1] равен и параллелен [С1D1].
70. Если 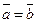 , то
, то 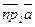 =
= 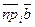 .
.
Доказательство. Так как равные векторы имеют равные векторные проекции, то при сложении первый вектор можно отложить от любой точки. Пусть О Î l, 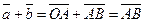 . Если А ® А1, В ® В1, то . Если А ® А1, В ® В1, то 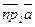 = = 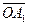 , , 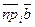 = = 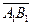 , , 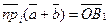 . Так как . Так как 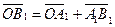 , то , то 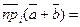 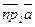 + + 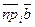 . .
| 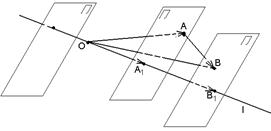 Рис. 11
Рис. 11
|
80.  = a ×
= a ×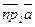 . (Докажите самостоятельно)
. (Докажите самостоятельно)
 2014-01-25
2014-01-25 897
897








