На плоскости
Дано:R = 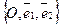 , М0(х0, у0), , М0(х0, у0), 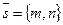 , , 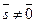 , l ' M0, l ½½ , l ' M0, l ½½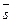 .
Найти условие, определяющее l.
Пусть М(х, у). .
Найти условие, определяющее l.
Пусть М(х, у).
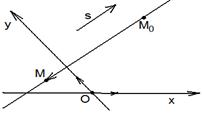 Рис. 30
М Î l Û
Рис. 30
М Î l Û 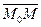 коллинеарен коллинеарен 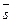 Û
либо 1) Û
либо 1) 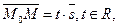 либо 2) координаты
либо 2) координаты 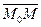 и и 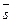 пропорциональны.
Рассмотрим оба случая.
1) М Î l Û пропорциональны.
Рассмотрим оба случая.
1) М Î l Û 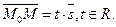 Если Если 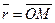 , , 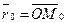 , то получим , то получим
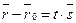 (14)
Это векторное уравнение прямой, проходящей через данную точку параллельно данному вектору.
Перепишем в координатах. Получим (14)
Это векторное уравнение прямой, проходящей через данную точку параллельно данному вектору.
Перепишем в координатах. Получим
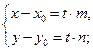 Отсюда Отсюда 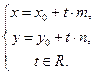 (15)
В полученных уравнениях t называется параметром, а уравнения – параметрическими уравнениями прямой, проходящей через данную точку параллельно данному вектору.
2) М Î l Û координаты (15)
В полученных уравнениях t называется параметром, а уравнения – параметрическими уравнениями прямой, проходящей через данную точку параллельно данному вектору.
2) М Î l Û координаты 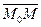 и и 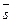 пропорциональны Û пропорциональны Û 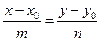 (16).
Это канонические уравнения прямой, проходящей через данную точку параллельно данному вектору. (16).
Это канонические уравнения прямой, проходящей через данную точку параллельно данному вектору.
| В пространстве
Дано:R = 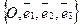 , М0(х0, у0, z0), , М0(х0, у0, z0), 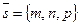 , , 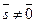 , l ' M0, l ½½ , l ' M0, l ½½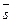 .
Найти условие, определяющее l.
Пусть М(х, у, z). .
Найти условие, определяющее l.
Пусть М(х, у, z).
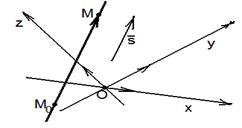 Рис. 301
М Î l Û
Рис. 301
М Î l Û 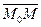 коллинеарен коллинеарен 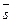 Û
либо 1) Û
либо 1) 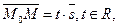 либо 2) координаты
либо 2) координаты 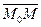 и и 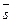 пропорциональны.
Рассмотрим оба случая.
1) М Î l Û пропорциональны.
Рассмотрим оба случая.
1) М Î l Û 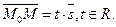 Если Если 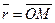 , , 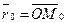 , то получим , то получим
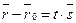 (141)
Это векторное уравнение прямой, проходящей через данную точку параллельно данному вектору.
Перепишем в координатах. Получим (141)
Это векторное уравнение прямой, проходящей через данную точку параллельно данному вектору.
Перепишем в координатах. Получим
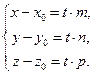 Отсюда Отсюда 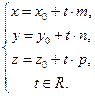 (151)
В полученных уравнениях t называется параметром, а уравнения – параметрическими уравнениями прямой, проходящей через данную точку параллельно данному вектору.
2) М Î l Û координаты (151)
В полученных уравнениях t называется параметром, а уравнения – параметрическими уравнениями прямой, проходящей через данную точку параллельно данному вектору.
2) М Î l Û координаты 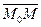 и и 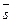 пропорциональны Û пропорциональны Û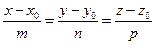 (161) Это канонические уравнения прямой, проходящей через данную точку параллельно данному вектору. (161) Это канонические уравнения прямой, проходящей через данную точку параллельно данному вектору.
|
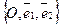 , М0(х0, у0),
, М0(х0, у0), 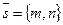 ,
, 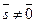 , l ' M0, l ½½
, l ' M0, l ½½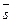 .
Найти условие, определяющее l.
Пусть М(х, у).
.
Найти условие, определяющее l.
Пусть М(х, у).
 Рис. 30
М Î l Û
Рис. 30
М Î l Û 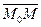 коллинеарен
коллинеарен 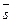 Û
либо 1)
Û
либо 1) 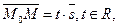 либо 2) координаты
либо 2) координаты 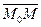 и
и 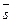 пропорциональны.
Рассмотрим оба случая.
1) М Î l Û
пропорциональны.
Рассмотрим оба случая.
1) М Î l Û 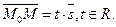 Если
Если 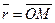 ,
, 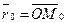 , то получим
, то получим
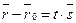 (14)
Это векторное уравнение прямой, проходящей через данную точку параллельно данному вектору.
Перепишем в координатах. Получим
(14)
Это векторное уравнение прямой, проходящей через данную точку параллельно данному вектору.
Перепишем в координатах. Получим
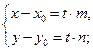 Отсюда
Отсюда 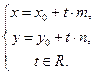 (15)
В полученных уравнениях t называется параметром, а уравнения – параметрическими уравнениями прямой, проходящей через данную точку параллельно данному вектору.
2) М Î l Û координаты
(15)
В полученных уравнениях t называется параметром, а уравнения – параметрическими уравнениями прямой, проходящей через данную точку параллельно данному вектору.
2) М Î l Û координаты 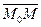 и
и 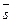 пропорциональны Û
пропорциональны Û 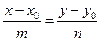 (16).
Это канонические уравнения прямой, проходящей через данную точку параллельно данному вектору.
(16).
Это канонические уравнения прямой, проходящей через данную точку параллельно данному вектору.
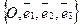 , М0(х0, у0, z0),
, М0(х0, у0, z0), 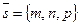 ,
, 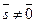 , l ' M0, l ½½
, l ' M0, l ½½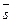 .
Найти условие, определяющее l.
Пусть М(х, у, z).
.
Найти условие, определяющее l.
Пусть М(х, у, z).
 Рис. 301
М Î l Û
Рис. 301
М Î l Û 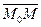 коллинеарен
коллинеарен 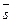 Û
либо 1)
Û
либо 1) 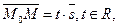 либо 2) координаты
либо 2) координаты 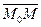 и
и 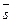 пропорциональны.
Рассмотрим оба случая.
1) М Î l Û
пропорциональны.
Рассмотрим оба случая.
1) М Î l Û 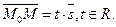 Если
Если 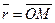 ,
, 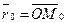 , то получим
, то получим
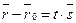 (141)
Это векторное уравнение прямой, проходящей через данную точку параллельно данному вектору.
Перепишем в координатах. Получим
(141)
Это векторное уравнение прямой, проходящей через данную точку параллельно данному вектору.
Перепишем в координатах. Получим
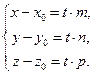 Отсюда
Отсюда 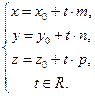 (151)
В полученных уравнениях t называется параметром, а уравнения – параметрическими уравнениями прямой, проходящей через данную точку параллельно данному вектору.
2) М Î l Û координаты
(151)
В полученных уравнениях t называется параметром, а уравнения – параметрическими уравнениями прямой, проходящей через данную точку параллельно данному вектору.
2) М Î l Û координаты 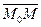 и
и 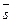 пропорциональны Û
пропорциональны Û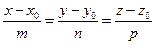 (161) Это канонические уравнения прямой, проходящей через данную точку параллельно данному вектору.
(161) Это канонические уравнения прямой, проходящей через данную точку параллельно данному вектору.
 2014-01-25
2014-01-25 883
883








