Прямая в прямоугольной системе координат на плоскости
Дано: R = 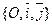 , М0(х0, у0), , М0(х0, у0), 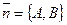 , , 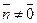 , l ' M0, l ^ , l ' M0, l ^ 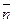 . Найти уравнение l. Найти уравнение l – это значит найти условие, которому удовлетворяют координаты любой точки прямой и не удовлетворяют координаты никаких других точек. М Î l Û либо . Найти уравнение l. Найти уравнение l – это значит найти условие, которому удовлетворяют координаты любой точки прямой и не удовлетворяют координаты никаких других точек. М Î l Û либо 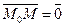 , либо , либо 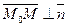 Û Û 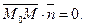 (*) Так как (*) Так как 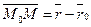 , то (*) перепишется , то (*) перепишется | 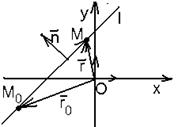 Рис. 20 Рис. 20 |
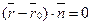 (24)
(24)
Полученное уравнение – это векторное уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.
Переписав уравнение (24) в координатах, получим
А(х - х0) + В(у - у0) = 0 (25)
Поставим обратную задачу:
Дано: R = 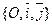 , l: A x + B y + C = 0 (*).
, l: A x + B y + C = 0 (*).
Доказать: если 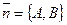 , то
, то 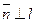 .
.
Доказательство. Пусть М(х, у) – произвольная точка данной прямой и М0(х0, у0) – некоторая фиксированная её точка. Тогда А х0 + В у0 + С = 0. Вычитая почленно полученное тождество из уравнения (*), получим уравнение А(х - х0) + В(у - у0) = 0, эквивалентное уравнению (*), т.е. уравнение (25). Если 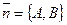 , то (25) можно записать
, то (25) можно записать 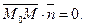 Вектор
Вектор 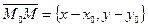 либо нулевой, либо параллелен l. Так как
либо нулевой, либо параллелен l. Так как 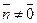 , то для всех точек М Î l, отличных от М0, имеет место
, то для всех точек М Î l, отличных от М0, имеет место 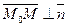 . Отсюда следует, что
. Отсюда следует, что 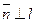 .
.
|
|
|
2.3.2. Уравнение прямой, проходящей через данную точку под данным углом к оси (Ох)
Дано: R = 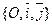 , М0(х0, у0), l ' М0, , М0(х0, у0), l ' М0, 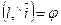 (угол j ориентированный). Найти уравнение l. Для решения задачи достаточно знать вектор, параллельный данной прямой. Возьмём вектор (угол j ориентированный). Найти уравнение l. Для решения задачи достаточно знать вектор, параллельный данной прямой. Возьмём вектор 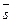 такой, что такой, что 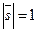 и и 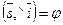 . Очевидно, . Очевидно, 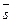 ½½ l. Так как координаты вектора в прямоугольной системе координат равны ортогональным ½½ l. Так как координаты вектора в прямоугольной системе координат равны ортогональным | 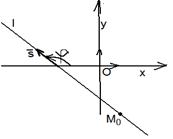 Рис. 21 Рис. 21 |
проекциям этого вектора на соответствующие оси, то 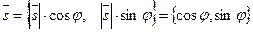 . Используя каноническое уравнение прямой на плоскости (16), получим
. Используя каноническое уравнение прямой на плоскости (16), получим
l: 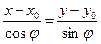 (26)
(26)
Прямые, не перпендикулярные оси (О х) называются наклонными. Для таких прямых 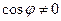 , следовательно, уравнение (26) можно привести к виду
, следовательно, уравнение (26) можно привести к виду
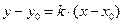 , где
, где 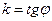 (27)
(27)
Если l ^ (О х), то уравнение (26) можно привести к виду х = х0 (28) Это уравнение вертикальной прямой.
Если l – наклонная прямая и l Ç (О у) = В, где В(0, в), то уравнение (27) преобразуется к виду у = к×х + в (29)
Уравнение (29) называют уравнение прямой с угловым коэффициентом. В этом уравнении к – тангенс угла наклона прямой к оси (О х), в – отрезок, отсекаемый прямой на оси (О у).
 2014-01-25
2014-01-25 1245
1245
