2014-01-25
861
Если в каноническом уравнении эллипса, гиперболы или параболы заменить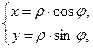 
то получим уравнение соответствующей линии в той системе полярных координат, полюс которой совпадает с началом ПДСК, а полярная ось совпадает с осью (ОЗ). Уравнения, очевидно, будут различными. Но существует такая система полярных координат, в которой уравнения всех трёх линии имеют одинаковый вид.
Зададим систему полярных координат так, что а) в случае эллипса полюс совпадает с фокусом F1, а полярн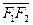ая ось имеет направление 
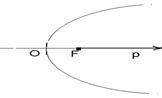
; б) в случае гиперболы полюс совпадает с фокусом F2, а полярная ось имеет направление 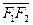; в) в случае параболы полюс совпадает с её единственным фокусом, а полярная ось направлена по оси параболы в сторону от её вершины (рис. 15).
| 
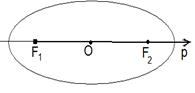
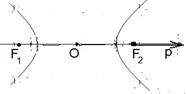Рис. 15
| 
|
Пусть для эллипса, параболы или «правой» ветви гиперболы (обозначим их w) зафиксирована указанная система полярных координат, пусть М(r, j) и пусть t – директриса, соответствующая выбранному фокусу. Тогда М Î w Û 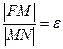 (рис. 16)
½FМ½ = r, ½МN½ = ½МК½ + ½КN½, ½МК½= r×соsj,
| 
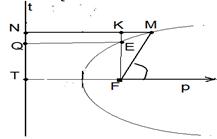Рис. 16
|
½NК½ = ½QЕ½, ½EF½: ½QЕ½= e, т.к. точка Е лежит на w. Если обозначить ½EF½= h, то ½QЕ½=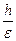 
. Следовательно, ½МN½= r×соsj + 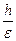. Итак, М Î w Û 
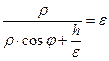. Преобразуя это уравнение, получим 
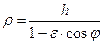(8)
При e < 1 уравнение (8) задаёт эллипс, при e > 1 оно задаёт «правую» ветвь гиперболы, при e = 1 – параболу.
Для эллипса и гиперболы Е(-с,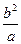 
). Следовательно, h = 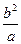. Для параболы (если её уравнение у2 = 2рх) h = р.
