Определение 8. Параболой называется множество всех точек плоскости, каждая из которых равноудалёна от данной точки и от данной прямой (данная точка не лежит на данной прямой).
Данная точка F называется фокусом параболы, а данная прямая t – её директрисой.
Выберем прямоугольную систему координат так, чтобы ось (ОХ) проходила через фокус перпендикулярно директрисе в сторону от директрисы к фокусу. За начало координат возьмём середину отрезка между директрисой и фокусом (рис. 12). М Î параболе Û úFМú = d(М, t) (*). Обозначим d(F, t) = р. Тогда F(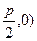 и прямая t будет иметь и прямая t будет иметь | 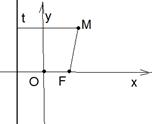 Рис. 12 Рис. 12 |
уравнение х = 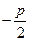 . Равенство (*) перепишется
. Равенство (*) перепишется 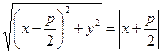 . Получили уравнение параболы. Так как обе части равенства неотрицательны, то возведение в квадрат даст эквивалентное уравнение
. Получили уравнение параболы. Так как обе части равенства неотрицательны, то возведение в квадрат даст эквивалентное уравнение
у2 = 2рх (7).
Полученное уравнение называется каноническим уравнением параболы. В этом уравнении р > 0. Из уравнения (7) следуют свойства:
| · парабола лежит в той полуплоскости с границей (ОУ), в сторону которой направлена ось (ОХ); · парабола симметрична относительно оси (ОХ); · при х ® ¥ ½у½ ® ¥; · парабола проходит через начало координат и не имеет других точек пересечения с осями координат. Начало координат называется вершиной параболы. | 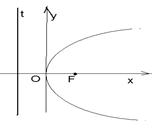 Рис. 13 Рис. 13 |
Если М0(х0, у0) Î параболе, то уравнение касательной к параболе в этой точке имеет вид уу0 = р(х + х0).
Теорема 7. Любые две параболы подобны.
Доказательство. Пусть у2 = 2рх и у2 = 2р1х - две параболы. Пусть у = кх – любая прямая, проходящая через начало координат. Пусть эта прямая пересекает параболы в точках М и N. Тогда, если прямая проходит в первом координатном углу, М(х1,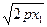 ), N(х2, ), N(х2, 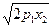 ). Так как М и N лежат на данной прямой, то у1 = кх1, у2 = кх2. Следовательно, ). Так как М и N лежат на данной прямой, то у1 = кх1, у2 = кх2. Следовательно, 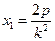 , , 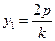 , , | 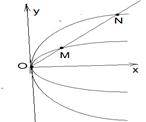 Рис. 14 Рис. 14 |
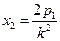 ,
, 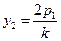 . Отсюда
. Отсюда 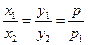 , т.е. параболы подобны с коэффициентом подобия
, т.е. параболы подобны с коэффициентом подобия 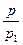 .
.
Замечание 1. Если вершиной параболы является точка С(х0, у0) и ось параболы параллельна оси (ОХ), то парабола имеет уравнение (у – у0)2 = 2р(х – х0).
Замечание 2. Если в уравнении (7) р < 0, то парабола располагается в той полуплоскости с границей (ОУ), в которой лежит отрицательная полуось (ОХ). Уравнения х2 = 2ру при любом р задают параболы, симметричные относительно оси (ОУ).
Общие свойства эллипса, гиперболы и параболы описывает следующая
Теорема 8. Для любых данных прямой t и точки F (F Ï t) множество точек, отношение расстояний от каждой из которых до данной точки и до данной прямой есть постоянная величина e, есть либо эллипс, либо гипербола, либо парабола.
 2014-01-25
2014-01-25 1149
1149