Определение 13. Эллипсоидом называется множество точек пространства, которое в некоторой прямоугольной системе координат можно задать уравнением
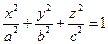 (30)
(30)
Из уравнения сразу следуют такие свойства эллипсоида:
· - а £ х £ а, - b £ у £ b, -с £ z £ с. Следовательно, эллипсоид лежит внутри прямоугольного параллелепипеда, симметричного относительно координатных плоскостей, длины рёбер которого равны 2 а, 2 b, 2 с;
· Эллипсоид симметричен относительно координатных плоскостей, координатных осей и начала координат.
Исследуем форму эллипсоида.
Если поверхность задана уравнением, то исследование её формы часто бывает удобно проводить методом сечений. Для этого исследуемую поверхность пересекают различными плоскостями, проще всего координатными и параллельными координатным.
I. Пересечём эллипсоид плоскостью, параллельной (ХОУ), её уравнение z = h. Уравнения сечения будут 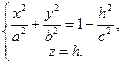 (*)
(*)
Возможны случаи:
1) -с < h < с. В этом случае система (*) определяет эллипс в плоскости z = h. Полуоси эллипса равны а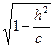 и b и b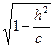 . Наибольшие полуоси получаются при h = 0, т.е. в плоскости (ХОУ). При h ® ± с полуоси стремятся к нулю, т.е. эллипс стягивается в точку.
2) h = ± с. В каждой из этих плоскостей система (*) определяет точку, т.е. плоскости z = ± с пересекают эллипсоид в одной точке каждая (рис.23). . Наибольшие полуоси получаются при h = 0, т.е. в плоскости (ХОУ). При h ® ± с полуоси стремятся к нулю, т.е. эллипс стягивается в точку.
2) h = ± с. В каждой из этих плоскостей система (*) определяет точку, т.е. плоскости z = ± с пересекают эллипсоид в одной точке каждая (рис.23).
| 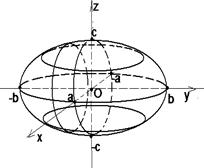 Рис. 23
Рис. 23
|
3) h > с или h < -с. В этом случае система (*) определяет пустое множество точек, т.е. плоскости z = h при указанных h не пересекают эллипсоид.
II. При пересечении эллипсоида плоскостями, параллельными (ХОZ) и (УОZ) получим аналогичные результаты. Проведите эти исследования самостоятельно.
 2014-01-25
2014-01-25 880
880








