Определение 14. Однополостным гиперболоидом называется множество точек пространства, которое в некоторой прямоугольной системе координат можно задать уравнением
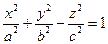 (31)
(31)
Из уравнения (31) следует
· 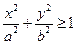 , т.е. гиперболоид лежит вне эллиптического цилиндра, образующие которого параллельны оси (ОZ);
, т.е. гиперболоид лежит вне эллиптического цилиндра, образующие которого параллельны оси (ОZ);
· Однополостный гиперболоид симметричен относительно координатных плоскостей, координатных осей и начала координат.
Исследуем форму этого гиперболоида методом сечений.
I. Пересечём гиперболоид плоскостью, параллельной (ХОУ), её уравнение z = h. Уравнения сечения будут 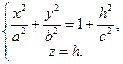 (**)
(**)
При любом h это уравнение определяет эллипс с полуосями а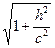 и b и b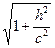 . Наименьший эллипс получается при h = 0, т.е. в плоскости (ХОУ). При возрастании ½h½ полуоси эллипсов увеличиваются и стремятся к бесконечности (рис. 24).
II. При пересечении гиперболоида плоскостями у = m, параллельными плоскости (УОZ). Уравнения сечений . Наименьший эллипс получается при h = 0, т.е. в плоскости (ХОУ). При возрастании ½h½ полуоси эллипсов увеличиваются и стремятся к бесконечности (рис. 24).
II. При пересечении гиперболоида плоскостями у = m, параллельными плоскости (УОZ). Уравнения сечений
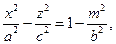 у = m. (***)
Возможны случаи:
1) -b < m < b. Сечениями будут гиперболы, действительные оси которых параллельны оси (ОХ) и полуоси имеют длину у = m. (***)
Возможны случаи:
1) -b < m < b. Сечениями будут гиперболы, действительные оси которых параллельны оси (ОХ) и полуоси имеют длину
| 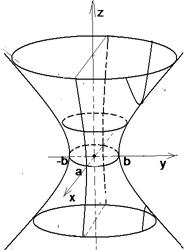 Рис. 24
Рис. 24
|
а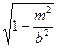 и b
и b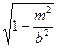 . Наибольшие полуоси получаются при m = 0. При увеличении ½m½ полуоси уменьшаются и стремятся к нулю. Следовательно, ветви гиперболы сближаются.
. Наибольшие полуоси получаются при m = 0. При увеличении ½m½ полуоси уменьшаются и стремятся к нулю. Следовательно, ветви гиперболы сближаются.
2)½m½ = b. В этом случае 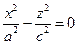 . Это уравнение определяет пару пересекающихся прямых. Итак, плоскости у = b и у = -b пересекают каждая гиперболоид по паре пересекающихся прямых.
. Это уравнение определяет пару пересекающихся прямых. Итак, плоскости у = b и у = -b пересекают каждая гиперболоид по паре пересекающихся прямых.
3) ½m½ > b. В этом случае уравнения (***) определяют гиперболу, действительная ось которой параллельна оси (ОZ). При увеличении ½m½ полуоси будут возрастать, следовательно, ветви гиперболы удаляются друг от друга (рис. 24).
III. При пересечении гиперболоида плоскостями х = n, параллельными плоскости (УОZ) получим результаты, аналогичные результатам предыдущего пункта (проведите это исследование сами).
 2014-01-25
2014-01-25 899
899








